|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Погрешность (математич.) | Погрешность (далее П) данного числа а, которое рассматривается как приближенное значение некоторой величины, точное значение которой равно х, есть разность х — а. Ее называют абсолютной погрешностью. Отношение х — а к а называют относительной погрешностью числа а. Для характеристики П (математич.) обычно пользуются указанием ее границ. Число D(а) такое, что ½х — a½ £ D(a), называют границей абсолютной П (математич.) Число d(a) такое, что 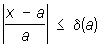 , называют границей относительной П (математич.) Границы относит. П (математич.) часто выражают в процентах. В качестве D(а) и d(а) берутся по возможности меньшие числа.
Информацию о том, что число а является приближенным значением числа х с границей абсолютной П (математич.) D(а), принято записывать в виде: х = а ± D(а). Аналогичное соотношение для относительной П (математич.) записывается в виде: х = а (1 ± d(а*(.
Границы абсолютной и относительной П (математич.) указывают на максимально возможное расхождение х и а. Наряду с ними часто употребляются характеристики П (математич.), учитывающие характер возникновения П (математич.) (см. Погрешности измерений) и частоту различных значений разности х и а. При таком подходе к П (математич.) используются методы теории вероятностей (см. Ошибок теория).
При численном решении задачи П (математич.) результата обусловливается неточностями, которые присущи формулировке задачи и способам ее решения. П (математич.), возникающую вследствие неточности математического описания реального процесса (в частности, неточности задания исходных данных), называют неустранимой П (математич.); возникающую вследствие неточности метода решения — П (математич.) метода; возникающую вследствие неточности вычислений — вычислительной П (математич.) (см. Округление).
В процессе вычислений исходные П (математич.) последовательно переходят от операции к операции, накапливаясь и порождая новые П (математич.) Возникновение и распространение П (математич.) в вычислениях являются предметом специальных исследований (см. Численные методы).
Лит.: Березин И. С., Жидков Н. П (математич.), Методы вычислений, 3 изд., т. 1, М., 1966; Бахвалов Н. С., Численные методы, М., 1973.
Г. Д. Ким.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.01.2025 22:27:42
|
|
|
|
|
|
|
|
|
|
|
