
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Повторного логарифма закон | Повторного логарифма закон (далее П) одна из предельных теорем теории вероятностей, близкая по смыслу к закону больших чисел (см. Больших чисел закон). П указывает при определенных условиях точный порядок роста сумм независимых случайных величин при увеличении числа слагаемых. Пусть, например, случайные величины X1, X2,..., Xn,... независимы и каждая из них принимает два значения: +1 или —1, каждое с вероятностью, равной 1/2, и пусть sn = X1 +... + Xn. Тогда с вероятностью, равной 1, при любом d > 0:
1) при всех n, больших некоторого (зависящего от случая) номера :
sn < (1 + d)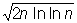
2) для бесконечной последовательности номеров n:
sn > (1 - d)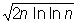 . .
Название "П" объясняется наличием в вышеприведенных выражениях множителя n. П возник из задач т. н. метрической теории чисел (см. Чисел теория). Первый результат, относящийся к П, был установлен в 1924 А. Я. Хинчиным. Дальнейшие существенные продвижения в изучении условий приложимости П связаны с работами А. Н. Колмогорова (1929) и В. Феллера (1943).
Лит.: Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.
Ю. В. Прохоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 18:16:07
|

|

|
 |
|

|
 |
 |
 |
|