|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Поверхность | Поверхность (далее П) одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придается различный смысл.
1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых П определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, П шара — множество точек, отстоящих на заданном расстоянии от данной точки. Понятие "П" лишь поясняется, а не определяется. Например, говорят, что П есть граница тела или след движущейся линии.
2) Математически строгое определение П основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Более точно, простой П называется образ гомеоморфного отображения (т. е. взаимно однозначного и взаимно непрерывного отображения) внутренности квадрата (см. Гомеоморфизм). Этому определению можно дать аналитическое выражение. Пусть на плоскости с прямоугольной системой координат u и u задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < u < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задается при помощи формул х = j(u, u), у = (u, u), z = c(u, u) (параметрические уравнения П). При этом от функций j(u, u), (u, u) и c(u, u) требуется, чтобы они были непрерывными и чтобы для различных точек (u, u) и (u`, u`) были различными соответствующие точки (x, у, z) и (x`, у`, z"). Примером простой П является полусфера. Вся же сфера не является простой П Это вызывает необходимость дальнейшего обобщения понятия П П, окрестность каждой точки которой есть простая П, называется правильной. С точки зрения топологического строения, П как двумерные многообразия разделяются на несколько типов: замкнутые и открытые, ориентируемые и неориентируемые и т.д. (см. Многообразие).
В дифференциальной геометрии исследуемые П обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости П, т. е. существования в каждой точке П определенной касательной плоскости, кривизны и т.д. Эти требования сводятся к тому, что функции j(u, u), (u, u), c(u, u) предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. Кроме того, требуется, чтобы в каждой точке хотя бы один из определителей
 ,  , 
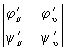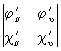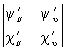
был отличен от нуля (см. Поверхностей теория).
В аналитической геометрии и в алгебраической геометрии П определяется как множество точек, координаты которых удовлетворяют определенному виду уравнений:
Ф (х, у, z) = 0. (*)
Таким образом, определенная П может и не иметь наглядного геометрического образа. В этом случае для сохранения общности говорят о мнимых П Например, уравнение
х2 + у2 + z2 + 1 = 0
определяет мнимую сферу, хотя в действительном пространстве нет ни одной точки, координаты которой удовлетворяют такому уравнению (см. также Поверхности второго порядка). Если функция Ф (х, у, z) непрерывна в некоторой точке и имеет в ней непрерывные частные производные 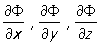 , из которых хотя бы одна не обращается в нуль, то в окрестности этой точки П, заданная уравнением (*), будет правильной П |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.12.2024 17:16:09
|
|
|
|
|
|
|
|
|
|
|
