
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Аффинные преобразования | Аффинные преобразования (далее А)точечные взаимно однозначные отображения плоскости (пространства) на себя, при которых прямые переходят в прямые. Если на плоскости задана декартова система координат, то любое Аффинные преобразования этой плоскости может быть определено посредством т. н. невырожденного линейного преобразования координат х и у точек этой плоскости. Такое преобразование задается формулами х" = ах + bу + р, y" = cx + dy + q с дополнительным требованием
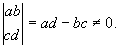
Аналогично, любое А. пространства может быть определено при помощи невырожденных линейных преобразований координат точек пространства. Совокупность всех Аффинные преобразования плоскости (пространства) на себя образует группу Аффинные преобразования Это означает, в частности, что последовательное проведение двух Аффинные преобразования эквивалентно некоторому одному Аффинные преобразования
Примерами Аффинные преобразования могут служить ортогональное прообразование (это преобразование представляет собой движение плоскости или пространства или движение с зеркальным отражением); преобразование подобия; равномерное "сжатие" (рис.). Равномерное "сжатие" с коэффициентом k плоскости p к расположенной на ней прямой а — преооразование, при котором точки а остаются на месте, а каждая не лежащая на а точка М плоскости p смещается по лучу, проходящему через М перпендикулярно а, в такую точку M", что отношение расстояний от М и М "до а равно k; аналогично определяется равномерное "сжатие" пространства к плоскости. Всякое Аффинные преобразования плоскости можно получить, выполнив некоторое ортогональное преобразование и последовательное "сжатие" к некоторым двум перпендикулярным прямым. Любое Аффинные преобразования пространства можно осуществить посредством некоторого ортогонального преобразования и последовательных "сжатии" к некоторым трем взаимно перпендикулярным плоскостям. При Аффинные преобразования параллельные прямые и плоскости преобразуются в параллельные прямые и плоскости. Свойства Аффинные преобразования широко используются в различных разделах математики, механики и теоретической физики. Так, в геометрии Аффинные преобразования применяются для т. н. аффинной классификации фигур. В механике Аффинные преобразования пользуются при изучении малых деформаций непрерывной сплошной среды; при таких деформациях малые элементы среды в первом приближении подвергаются Аффинные преобразования
Лит.: Мусхелишвили Н. И., Курс аналитической геометрии, 4 изд., М., 1967; Александров П. С., Лекции по аналитической геометрии, М. , 1968; Ефимов Н. В., Высшая геометрия, 4 изд., М., 1961.
Э. Г. Позняк.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:01:13
|

|

|
 |
|

|
 |
 |
 |
|