
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Периодические решения | Периодические решения (далее П) уравнений, решения, описывающие правильно повторяющиеся процессы. Для теории колебаний, небесной механики и др. наук особый интерес представляют П системы дифференциальных уравнений
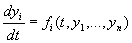 , i = 1,..., n (1) , i = 1,..., n (1)
Это такие решения yi = ji (t), которые состоят из периодических одного и того же периода функций независимого переменного t, то есть для всех значений t
ji (t + t) = ji (t)
где t > 0—период решения. Если система (1) стационарна, то есть функции fi = i (yi,.... yn), где i = 1,..., n, явным образом не зависят от t, то в фазовом пространстве (yi,..., yi) П отвечают замкнутые траектории. В частном случае эти траектории могут вырождаться в точки покоя 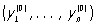 , где , где 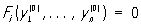 , которым соответствуют тривиальные (постоянные) П Что касается нетривиальных П, то задача о нахождении их решена лишь для дифференциальных уравнений специальных типов. , которым соответствуют тривиальные (постоянные) П Что касается нетривиальных П, то задача о нахождении их решена лишь для дифференциальных уравнений специальных типов.
В теории нелинейных колебаний особое значение имеет система двух уравнений
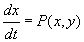 , , 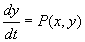 (2) (2)
фазовым пространством которой является плоскость (х, у). Точки покоя системы (2) находятся из системы уравнений: Р (х, у) = 0, Q (x, у) = 0. Система (2) заведомо не допускает нетривиальных П, если 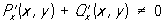 (критерий Бендиксона). Обычным приемом обнаружения нетривиальных П системы (2) (если они существуют) является построение такой ограниченной кольцеобразной области (см. рис.), что все траектории входят в нее при t ® +¥ или при t ® -¥; если область К не содержит точек покоя системы (2), то в К обязательно найдется замкнутая траектория, которой соответствует нетривиальное П (принцип Пуанкаре — Бендиксона). Другой подход к обнаружению П дает изучение поведения решений в окрестностях особых точек; именно, в окрестности центра интегральные кривые системы (2) замкнуты и им соответствуют нетривиальные П (критерий Бендиксона). Обычным приемом обнаружения нетривиальных П системы (2) (если они существуют) является построение такой ограниченной кольцеобразной области (см. рис.), что все траектории входят в нее при t ® +¥ или при t ® -¥; если область К не содержит точек покоя системы (2), то в К обязательно найдется замкнутая траектория, которой соответствует нетривиальное П (принцип Пуанкаре — Бендиксона). Другой подход к обнаружению П дает изучение поведения решений в окрестностях особых точек; именно, в окрестности центра интегральные кривые системы (2) замкнуты и им соответствуют нетривиальные П
Лит.: Немыцкий В. В. и Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.— Л., 1949; Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959; Стокер Дж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 17:04:06
|

|

|
 |
|

|
 |
 |
 |
|