
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Перестановочные соотношения | Перестановочные соотношения (далее П) коммутационные соотношения, фундаментальные соотношения в квантовой механике, устанавливающие связь между последовательными действиями на волновую функцию (или вектор состояния) двух операторов (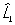 и и 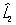 ), расположенных в разном порядке (то есть ), расположенных в разном порядке (то есть 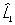 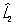 и и 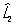 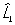 ). П определяют алгебру операторов (q-чисел; см. Операторы в квантовой теории). Если два оператора переставимы (коммутируют), то есть ). П определяют алгебру операторов (q-чисел; см. Операторы в квантовой теории). Если два оператора переставимы (коммутируют), то есть 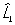 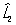 = = 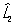 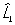 , то соответствующие им физические величины L1 и L2 могут иметь одновременно определенные значения. Если же их действие в разном порядке отличается численным фактором, то есть , то соответствующие им физические величины L1 и L2 могут иметь одновременно определенные значения. Если же их действие в разном порядке отличается численным фактором, то есть 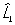 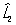 - - 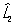 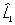 = c, то между соответствующими физическими величинами имеет место неопределенностей соотношение DL1DL2 £ |с|/2, где DL1 и DL2 - неопределенности (дисперсии) измеряемых значений физических величин L1 и L2. Важнейшими в квантовой механике являются П между операторами обобщенной координаты = c, то между соответствующими физическими величинами имеет место неопределенностей соотношение DL1DL2 £ |с|/2, где DL1 и DL2 - неопределенности (дисперсии) измеряемых значений физических величин L1 и L2. Важнейшими в квантовой механике являются П между операторами обобщенной координаты 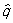 и сопряженного ей обобщенного импульса и сопряженного ей обобщенного импульса 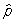 : : 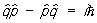 , где , где 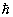 - постоянная Планка. Если оператор - постоянная Планка. Если оператор 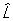 переставим с оператором полной энергии системы (гамильтонианом) переставим с оператором полной энергии системы (гамильтонианом) 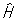 , то есть , то есть 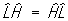 , то физическая величина L (ее среднее значение, дисперсия и т.д.) сохраняет свое значение во времени. , то физическая величина L (ее среднее значение, дисперсия и т.д.) сохраняет свое значение во времени.
В квантовой механике систем тождественных частиц и квантовой теории поля фундаментальное значение имеют П для операторов рождения а+ и поглощения а- частиц. Для системы свободных (невзаимодействующих) бозонов оператор рождения частицы в состоянии n, 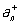 и оператор поглощения такой частицы, и оператор поглощения такой частицы, 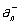 , удовлетворяют п. с. , удовлетворяют п. с. 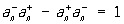 , а для фермионов , а для фермионов 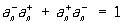 ; последнее П является формальным выражением Паули принципа. ; последнее П является формальным выражением Паули принципа.
В. Б. Берестецкий. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:54:11
|

|

|
 |
|

|
 |
 |
 |
|