
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Переменная | Переменная (далее П) переменное, одно из основных понятий математики и логики. Начиная с работ П Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников "высшей" математики под П понимали некоторую "величину", которая может "изменяться", принимая в процессе этого изменения различные "значения". Тем самым П противопоставлялись "постоянным" (или константам) — числам или каким-либо др. "величинам", каждая из которых имеет единственное, вполне определенное значение (см. Переменные и постоянные величины). По мере развития математики и в ходе ее обоснования представления о "процессах", "изменении величин" и т. п. тщательно изгонялись из математического арсенала как "внематематические", в результате чего П стала пониматься как обозначение для произвольного элемента рассматриваемой предметной области (например, области натуральных чисел или действительных чисел), то есть как родовое имя всей этой области (в отличие от констант — "собственных имен" для чисел или др. конкретных предметов рассматриваемой области). Этот пересмотр взглядов на понятие П был тесно связан с перестройкой математики на базе множеств теории, завершившейся в конце 19 в. При всей простоте и "естественности" такой перестройки она существенным образом опирается на так называемую абстракцию актуальной бесконечности, позволяющую рассматривать произвольные бесконечные множества в качестве "данных" ("завершенных", "готовых", "актуальных") объектов и применять по отношению к ним любые средства классической логики, отвлекаясь от незавершенности и принципиальной незавершимости процесса образования такого множества. Трудности решения логических проблем, связанных с принятием этой абстракции, делают понятной частичную "реабилитацию" старинных представлений о "переменных величинах"; при построении математических теорий представители некоторых школ (см. Математический интуиционизм, Конструктивное направление) предпочитают обходиться боле (слабой, но зато менее уязвимой в логическом отношении абстракцией потенциальной осуществимости, с точки зрения которой с бесконечными множествами как раз связываются представления о процессах их "порождения",— сколь угодно далеко заходящих, но никогда не завершающихся (см. Бесконечность в математике). При исследовании вопроса непротиворечивости различных областей математики на такую позицию фактически встает значительное большинство математиков и логиков (см. Метаматематика).
В формализованных языках (исчислениях, формальных системах) математической логики П называются символы строго фиксированного вида, могущие при определенных условиях заменяться выражениям данного исчисления. Это относится к так называемым свободным (или значащим) П примером которых может служить П в неравенстве х > 5, обращающемся при подстановке вместо х, скажем, цифры 7 (то есть обозначения для числа) 7 в истинное высказывание, а при подстановке цифры 2 — в ложное высказывание. Что касается так называемых связанных (или фиктивных) П, то они сами по себе вообще ничего не означают, несут чисто синтаксические функции и могут (при соблюдении некоторых элементарных предосторожностей) "переименовываться", то есть заменяться др. П Такова, например, П у в записях 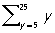 или "yP (y), в интерпретации (прочтения) которых она вообще не входит и может быть заменена любой др. П так, первая из них (читаемая как "сумма целых чисел от 5 до 25") может быть заменена на или "yP (y), в интерпретации (прочтения) которых она вообще не входит и может быть заменена любой др. П так, первая из них (читаемая как "сумма целых чисел от 5 до 25") может быть заменена на 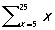 или или 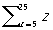 , а вторая ("все числа обладают свойством Р") на "tP (t). Различают индивидные, пропозициональные, предикатные, функциональные, числовые и др. виды П, вместо которых можно (согласно специальным правилам подстановки) подставлять соответственно обозначения предметов из рассматриваемой области ("термы"), обозначения для конкретных высказываний, предикатов, функций, чисел и др. Т. о., П можно содержательно понимать как "пустое место" в формуле, снабженное указанием, чем это "место" может быть "заполнено" (своего рода "тара под строго определенный товар"). , а вторая ("все числа обладают свойством Р") на "tP (t). Различают индивидные, пропозициональные, предикатные, функциональные, числовые и др. виды П, вместо которых можно (согласно специальным правилам подстановки) подставлять соответственно обозначения предметов из рассматриваемой области ("термы"), обозначения для конкретных высказываний, предикатов, функций, чисел и др. Т. о., П можно содержательно понимать как "пустое место" в формуле, снабженное указанием, чем это "место" может быть "заполнено" (своего рода "тара под строго определенный товар").
Свободные вхождения П в выражения содержательных научных теорий и формулы логико-математических исчислений (соответствующие употреблению неопределенных местоимений в обычной речи) допускают различные интерпретации. Первая (соответствующая применению всякого рода процедур подстановок) — так называемая предикатная интерпретация: формула A (x1,..., xn) какого-либо исчисления понимается как некоторый местный предикат. Та же формула может интерпретироваться и как предложение (высказывание), а именно как предложение "x1 … "xn A (x1 … xn), являющееся ее "замыканием",— это так называемая интерпретация всеобщности (употребительная, например, при формулировке аксиом различных научных теорий). Свободным П могут, наконец, приписываться значения, постоянные в пределах некоторого контекста (например, вывода из данной совокупности формул), их тогда называют параметрами этого контекста и говорят об их условной интерпретации. Например, П х в выражении cos х, взятом изолированно, имеет предикатную интерпретацию, в тождестве sin2x + cos2x = 1 — интерпретацию всеобщности, в уравнении cos х = 1 (в процессе его решения, когда эта П именуется "неизвестным") — условную интерпретацию.
Таким образом, на различных уровнях формализации понятие П выступает как уточнение средств, общеупотребительных в обычных разговорных языках (неопределенные местоимения, неопределенные артикли), и различных способов использования этих средств. См. также Квантор, Логика предикатов, Математика. Лит.: Клини С. К, Введение в метаматематику, пер с англ, М., 1957, §§ 31, 32, 45, Черч А, Введение в математическую логику, пер с англ, т. 1, М., 1960, §§ 02, 04, 06. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:54:26
|

|

|
 |
|

|
 |
 |
 |
|