
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Перевала метод | Перевала метод (далее П) метод нахождения асимптотических выражений некоторых интегралов. Многие специальные функции (например, цилиндрические функции, сферические функции и др.) выражаются интегралами вида
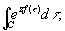 (*) (*)
где f (t) = u (х, у) + iu(x, y) - аналитическая функция от t = х + iy такая, что u (х, у) стремится к - ¥ при приближении к концам контура С. Для вычисления этих интегралов при больших положительных значениях z применяется П Он состоит в том, что контур С деформируют в контур ", имеющий те же концы, что и С, и проходящий через нуль t0 функции f"(t) по кривой вида u(x, y) = const (по теореме Коши значение интеграла не меняется при деформации контура). На поверхности t = u (х, у) контур " изобразится путем, проходящим через точку перевала этой поверхности (отсюда название метода) так, что по обе стороны этой точки путь как можно более круто спускается к большим отрицательным значениям u (х, у). Поэтому при действительном положительном z существенное влияние на значение интеграла (*) оказывает лишь ближайшая окрестность точки t0, и это обстоятельство может быть использовано для получения асимптотического выражений интеграла, например заменой функции f (t) в окрестности точки то отрезком ее ряда Тейлора.
П, как правило, дает возможность найти весь асимптотический ряд для интеграла (*).
Если подинтегральная функция многозначна, то при деформации контура приходится считаться с разрезами, возникающими в результате неоднозначности, и часть пути направлять вдоль разрезов. П применяется и к вычислению интегралов вида
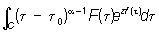 . .
Лит.: Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:59:30
|

|

|
 |
|

|
 |
 |
 |
|