|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Первообразный корень | Первообразный корень (далее П) по модулю m, такое число g, что положительное наименьшее число k, для которого разность gk — 1 делится на m (gk сравнимо с 1 по модулю m), совпадает c j(m), где j(m) — число натуральных чисел, меньших m и взаимно простых с m. Например, при m = 7 П по модулю 7 является число 3. Действительно j(7) = 6; числа 31 — 1 = 2, 32 — 1 = 8, 33 — 1 = 26, 34 — 1 = 80, 35 — 1 = 242 не делятся на 7, лишь 36 — 1 = 728 делится на 7. П существуют, когда m = 2, m = 4, m = рa, m = 2pa (где р — простое нечетное число, a — целое ³1), а для других модулей их нет. Число П в этих случаях равно j(j(m)) (числа, разность которых кратна m, не считаются за различные). И. М. Виноградов в 1926 установил, что в интервале (1, 22k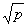 lnp) найдется П по модулю р, где р — простое нечетное число, k — число различных простых делителей числа р — 1. См. также Чисел теория, Индексы в теории чисел.
Лит.: Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; его же, Избр. труды. М., 1952, с. 54—57. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 12.01.2025 15:23:08
|
|
|
|
|
|
|
|
|
|
|
