
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Пелля уравнение | Пелля уравнение (далее П) уравнение вида x2 - 2 = 1 (D - целое положительное число), у которого разыскиваются решения в целых числах. Если D не является полным квадратом, то уравнение имеет бесконечное количество решений. Решение x0 = 1, y0 = 0 очевидно. Следующее по величине решение (x1, y1) П можно найти, пользуясь разложением в непрерывную дробь числа 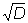 . Зная решение (x1, y1), всю совокупность решений (xn, yn) П получают из формулы: . Зная решение (x1, y1), всю совокупность решений (xn, yn) П получают из формулы:
(x1 + y1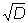 ) n = xn + yn ) n = xn + yn 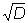 , ,
n = 0, 1, 2,...
Изучение П тесно связано с теорией алгебраических чисел. П названо по имени английского математика Дж. Пелля (J. Pell; 17 в.), которому Л. Эйлер по ошибке приписал один из способов решения этого уравнения. См. также Диофантовы уравнения.
Лит.: Венков Б. А., Элементарная теория чисел, М.- Л., 1937, гл. 2; Dickson L. E., History of the theory of numbers, v. 2, . ., 1966. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 17:03:54
|

|

|
 |
|

|
 |
 |
 |
|