
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Особая точка | Особая точка (далее О) в математике.
1) О кривой, заданной уравнением (x, у) = 0, - точка М0(х0, y0), в которой обе частные производные функции (x, у) обращаются в нуль:
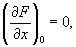 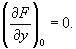
Если при этом не все вторые частные производные функции (x, у) в точке М0 равны нулю, то О называют двойной. Если наряду с обращением в нуль первых производных в точке М0 обращаются в нуль и все вторые производные, но не все третьи производные равны нулю, то О называется тройной, и т.д. При исследовании строения кривой вблизи двойной О важную роль играет знак выражения
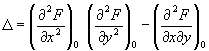 
Если D > 0, то О называется изолированной; например, у кривой у 2 - х 4 + 4x 2 = 0 начало координат есть изолированная О (см. рис. 1). Если D < 0, то О называется узловой, или точкой самопересечения; например, у кривой (x 2 + y 2 + a2)2 - 4a 2x 2 - a 4 = 0 начало координат есть узловая О (см. рис. 2). Если D = 0, то О кривой является либо изолированной, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную, например: а) точка возврата 1-го рода - различные ветви кривой расположены по разные стороны от общей касательной и образуют острие, как у кривой у 2 - х 3 = 0 (см. рис. 3, a); б) точка возврата 2-го рода - различные ветви кривой расположены по одну сторону от общей касательной, как у кривой (у - x 2)2 - х 5 = 0 (см. рис. 3, б); в) точка самоприкосновения (для кривой у 2 - х 4 = 0 начало координат является точкой самоприкосновения; (см. рис. 3, в). Наряду с указанными О имеется много других О со специальными названиями; например, асимптотическая точка - вершина спирали с бесконечным числом витков (см. рис. 4), точка прекращения, угловая точка и т.д.
Лит. см. при ст. Дифференциальная геометрия.
2) О дифференциального уравнения - точка, в которой одновременно обращаются в нуль и числитель и знаменатель правой части дифференциального уравнения
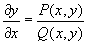 , (1) , (1)
где Р и Q - непрерывно дифференцируемые функции. Предполагая О расположенной в начале координат и используя Тейлора формулу, можно представить уравнение (1) в виде
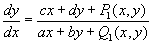 , ,
где 1(x, у) и Q1(x, у)- бесконечно малые по отношению к 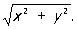 Характер поведения интегральных кривых около О зависит от корней l1 и l2 характеристического уравнения Характер поведения интегральных кривых около О зависит от корней l1 и l2 характеристического уравнения
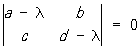 . .
Именно, если l1 ¹ l2 и l1l2 > 0 или l1 = l2, то О есть узел; все интегральные кривые, проходящие через точки достаточно малой окрестности узла, входят в него. Если l1 ¹ l2 и l1l2 < 0, то О есть седло; в окрестности седла четыре интегральные кривые (сепаратрисы) входят в О, а между ними располагаются интегральные кривые типа гипербол. Если l1,2 = a ± i b, a ¹ 0 и b ¹ 0, то О есть фокус; все интегральные кривые, проходящие через точки достаточно малой окрестности фокуса, представляют собой спирали с бесконечным числом витков в любой сколь угодно малой окрестности фокуса. Если, наконец, l1,2 = ± i b, b ¹ 0, то характер О не определяется одними линейными членами в разложениях Р (х, у) и Q (x, у), как это имело место во всех перечисленных случаях; здесь О может быть фокусом или центром, а может иметь и более сложный характер. В окрестности центра все интегральные кривые являются замкнутыми и содержат центр внутри себя. Так, например, точка (0, 0) является узлом для уравнений у " = 2у/х (l1 = 1, l2 = 2; см. рис. 5, а) и y " = у/х (l1 = l2 = 1; см. рис. 5, б), седлом для уравнения у" = -у/х (l1 = -1, l2 = 1; см. рис. 6), фокусом для уравнения у" = (х + у) / (х - у) (l1 = 1 - i, l2 = 1 + i; см. рис. 7) и центром для уравнения у" = -x / y (l1 = -i, l2 = i; см. рис. 8).
Если 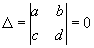 , то О называют особой точкой высшего порядка. О высшего порядка могут принадлежать к указанным типам, но могут иметь и более сложный характер. В случае, когда функции Р (х, у) и Q (х, у) аналитические, окрестность О высшего порядка может распадаться на области: D1 - заполненные интегральными кривыми, обоими концами входящими в О (эллиптические области), D2 - заполненные интегральными кривыми, одним концом входящими в О (параболические области), и D3 - области, ограниченные двумя интегральными кривыми, входящими в О, между которыми расположены интегральные кривые типа гипербол (гиперболические области) (см. рис. 9). Если нет интегральных кривых, входящих в О, то О называется точкой устойчивого типа. Окрестность устойчивой О состоит из замкнутых интегральных кривых, содержащих О внутри себя, между которыми расположены спирали (см. рис. 10). , то О называют особой точкой высшего порядка. О высшего порядка могут принадлежать к указанным типам, но могут иметь и более сложный характер. В случае, когда функции Р (х, у) и Q (х, у) аналитические, окрестность О высшего порядка может распадаться на области: D1 - заполненные интегральными кривыми, обоими концами входящими в О (эллиптические области), D2 - заполненные интегральными кривыми, одним концом входящими в О (параболические области), и D3 - области, ограниченные двумя интегральными кривыми, входящими в О, между которыми расположены интегральные кривые типа гипербол (гиперболические области) (см. рис. 9). Если нет интегральных кривых, входящих в О, то О называется точкой устойчивого типа. Окрестность устойчивой О состоит из замкнутых интегральных кривых, содержащих О внутри себя, между которыми расположены спирали (см. рис. 10).
Изучение О дифференциальных уравнений, т. е. по существу изучение поведения семейств интегральных кривых в окрестности О, составляет один из разделов качественной теории дифференциальных уравнений и играет важную роль в приложениях, в частности в вопросах устойчивости движения (работы А. М. Ляпунова, А. Пуанкаре и др.).
Лит. см. при ст. Дифференциальные уравнения.
3) О однозначной аналитической функции - точка, в которой нарушается аналитичность функции (см. Аналитические функции). Если существует окрестность О a, свободная от других О, то точку а называют изолированной О Если а - изолированная О и существует конечный 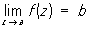 , то a называют устранимой О Путем надлежащего изменения определения функции в точке а (или доопределения ее в этой точке, если функция в ней вообще не определена), именно, полагая f (a) = b, можно добиться того, что a станет обыкновенной точкой исправленной функции. Например, точка z = 0 является устранимой О для функции , то a называют устранимой О Путем надлежащего изменения определения функции в точке а (или доопределения ее в этой точке, если функция в ней вообще не определена), именно, полагая f (a) = b, можно добиться того, что a станет обыкновенной точкой исправленной функции. Например, точка z = 0 является устранимой О для функции 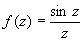 , так как , так как 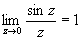 ; для функции f 1(z) = f (z), если z ¹ 0, и f1(0), = 1, точка z = 0 является обыкновенной точкой (f 1(z) аналитична в точке z = 0). Если а - изолированная О и ; для функции f 1(z) = f (z), если z ¹ 0, и f1(0), = 1, точка z = 0 является обыкновенной точкой (f 1(z) аналитична в точке z = 0). Если а - изолированная О и 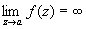 , то а называют полюсом или несущественно особой точкой функции f (z), если же , то а называют полюсом или несущественно особой точкой функции f (z), если же 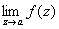 не существует, то существенно особой точкой. Ряд Лорана (см. Лорана ряд) функции f (z) в окрестности изолированной О не содержит отрицательных степеней z - а, если а - устранимая О, содержит конечное число отрицательных степеней z - а, если а - полюс (при этом порядок полюса р определяется как наивысшая степень не существует, то существенно особой точкой. Ряд Лорана (см. Лорана ряд) функции f (z) в окрестности изолированной О не содержит отрицательных степеней z - а, если а - устранимая О, содержит конечное число отрицательных степеней z - а, если а - полюс (при этом порядок полюса р определяется как наивысшая степень 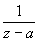 , встречающаяся в ряде Лорана), и содержит как угодно высокие степени , встречающаяся в ряде Лорана), и содержит как угодно высокие степени 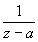 , если а - существенно особая точка. Например, для функции , если а - существенно особая точка. Например, для функции
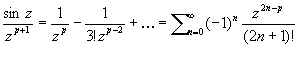 (p = 2, 3, …) (p = 2, 3, …)
точка z = 0 является полюсом порядка р, для функции
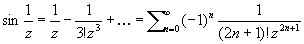
точка z = 0 является существенно особой точкой.
На границе круга сходимости степенного ряда должна находиться по крайней мере одна О функции, представляемой внутри этого круга данным степенным рядом. Все граничные точки области существования однозначной аналитической функции (естественной границы) являются О этой функции. Так, все точки единичного круга | z | = 1 являются особыми для функции
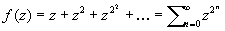 . .
Для многозначной аналитической функции понятие "О" более сложно. Помимо О, в отдельных листах римановой поверхности функции (то есть О однозначных аналитических элементов) всякая точка ветвления также является О функции. Изолированные точки ветвления римановой поверхности (то есть такие точки ветвления, что в некоторой их окрестности ни в одном листе нет других О функции) классифицируются следующим образом. Если а - изолированная точка ветвления конечного порядка и существует конечный 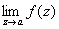 , то О называют обыкновенной критической точкой; если же , то О называют обыкновенной критической точкой; если же 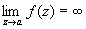 , то а называют критическим полюсом. Если а - изолированная точка ветвления бесконечного порядка и , то а называют критическим полюсом. Если а - изолированная точка ветвления бесконечного порядка и 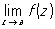 существует (конечный или бесконечный), то а называют трансцендентной О Все остальные изолированные точки ветвления называют критическими существенно особыми точками. Примеры: точка z = 0 является обыкновенной критической точкой функции существует (конечный или бесконечный), то а называют трансцендентной О Все остальные изолированные точки ветвления называют критическими существенно особыми точками. Примеры: точка z = 0 является обыкновенной критической точкой функции 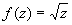 , критическим полюсом функции , критическим полюсом функции 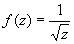 , трансцендентной О функции f (z) = ln z и критической существенно особой точкой функции f (z) = sin ln z. , трансцендентной О функции f (z) = ln z и критической существенно особой точкой функции f (z) = sin ln z.
Всякая О, кроме устранимой, является препятствием при аналитическом продолжении, т. е. аналитическое продолжение вдоль кривой, проходящей через неустранимую О, невозможно.
Лит. см. при ст. Аналитические функции.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 24.02.2026 19:33:58
|

|

|
 |
|

|
 |
 |
 |
|