
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Ортогональность | Ортогональность (далее О) (греч. orthogōnios — прямоугольный, от orthós — прямой и gōnía — угол), обобщение (часто синоним) понятия перпендикулярности. Если два вектора в трехмерном пространстве перпендикулярны, то их скалярное произведение равно нулю. Это позволяет обобщить понятие перпендикулярности, распространив его на векторы в любом линейном пространстве, в котором определено скалярное произведение, обладающее обычными свойствами (см. Гильбертово пространство), назвав два вектора ортогональными, если их скалярное произведение равно нулю. В частности, вводя скалярное произведение в пространстве комплекснозначных функций, заданных на отрезке (а, b ) формулой
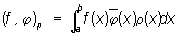 , ,
где r(х) ³ 0, называют две функции f (x) и j(x), для которых (f, j)r = 0, то есть
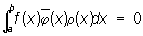 , ,
ортогональными с весом r(х). Два линейных подпространства называется ортогональными, если каждый вектор одного из них ортогонален каждому вектору другого. Это понятие обобщает понятие перпендикулярности двух прямых или прямой и плоскости в трехмерном пространстве (но не понятие перпендикулярности двух плоскостей). Термином ортогональные кривые обозначают кривые линии, пересекающиеся под прямым углом (измеряется угол между касательными в точке пересечения). См., например, ортогональные траектории в ст. Изогональные траектории.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 24.02.2026 19:50:47
|

|

|
 |
|

|
 |
 |
 |
|