|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Ортогональная матрица | Ортогональная матрица (далее О) порядка n матрица
 ,
произведение которой на транспонированную матрицу А" дает единичную матрицу, то есть АА" = Е (а следовательно, и A"A = Е). Элементы О удовлетворяют соотношениям:
 
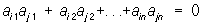
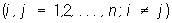
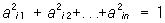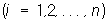
или эквивалентным соотношениям:
 
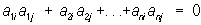
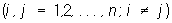
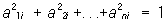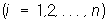
Определитель |A| О равен +1 или —1. При перемножении двух О снова получается О Все О порядка n относительно операции умножения образуют группу, называемую ортогональной. При переходе от одной прямоугольной системы координат к другой коэффициенты aij в формулах преобразования координат
 
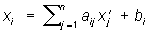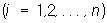
образуют О См. также Унитарная матрица.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 02.04.2025 04:28:30
|
|
|
|
|
|
|
|
|
|
|
