
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Ориентация (в геометрии) | Ориентация (далее О) обобщение понятия направления на прямой на геометрической фигуре более сложной структуры.
О на прямой. Точка может двигаться по прямой в двух противоположных направлениях. Например, по горизонтальной прямой АВ (рис. 1) возможно или движение справа налево, или движение слева направо. Прямая вместе с указанием определенного направления на ней называется ориентированной прямой.
О на кривой. Аналогично ориентации на прямой каждую замкнутую кривую можно ориентировать или против часовой стрелки (рис. 2), или по часовой стрелке (рис. 3).
О на плоскости. Пусть какой-либо кусок плоскости ограничен простой замкнутой кривой (т. е. замкнутой кривой без кратных точек). Эту кривую можно ориентировать двумя равными способами. При ориентации кривой ориентируется и ограниченный ею кусок плоскости. Две простые замкнутые кривые на плоскости считаются ориентированными одинаково, если при обходе этих кривых по указанному направлению ограниченные ими куски плоскости остаются с одной и той же стороны (в обоих случаях или справа, или слева). Например, на рис. 2 и 4 кривые ориентированы одинаково, а кривая на рис. 3 — противоположно первым двум. Достаточно выбрать на плоскости О (в геометрии) одной простой замкнутой кривой, чтобы тем самым определилась соответствующая О (в геометрии) всех остальных таких кривых, лежащих на той же плоскости. Плоскость вместе с определенным выбором О (в геометрии) лежащих на ней простых замкнутых кривых называются ориентированной плоскостью. Каждая плоскость может быть ориентирована двумя способами. О (в геометрии) плоскости может быть также задана при помощи выбора системы декартовых координат. Если на плоскости выбраны оси координат Ох и Оу с определенными положительными направлениями на них, то этому выбору соответствует О (в геометрии) плоскости, при которой окружность с центром в начале координат ориентирована в направлении от положительного направления оси Ox к положительному направлению оси Оу. Например, системы координат на рис. 5 и 6 определяют одну и ту же О (в геометрии) плоскости. Система же координат на рис. 7 ориентирована противоположным образом.
Координаты (x, у) и (х", у" ) в двух прямолинейных системах координат на плоскости связаны соотношениями
х"= a11x + a12y + b1
y` = a21x + a22y + b2 ,
где определитель
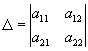
отличен от нуля. Системы координат (х, у) и (х", у") ориентированы одинаково, если D>0, и противоположно, если D<0. Это обстоятельство можно использовать для строгой аналитической теории О (в геометрии) на плоскости. Легко видеть, что множество всех прямолинейных систем координат распадается на два подмножества ` и " так, что в пределах ` (и в пределах ") все системы координат связаны преобразованиями с D>0, а любая система координат из ` связана с системой координат из " преобразованием с D<0. Выбрать О (в геометрии) плоскости - это и значит выбрать одно из множеств " или ”. Выбор О (в геометрии) на плоскости определяет знак расположенных на плоскости углов и площадей, ограниченных ориентированными замкнутыми кривыми. Например, формула
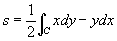
площади s, ограниченной замкнутой кривой с, ориентированной в направлении, указанном стрелкой, в случае правой системы координат (рис. 5 и 6) приведет к положительной площади для фигур рис. 2 и 4 и к отрицательной — для фигуры на рис. 3. Наоборот, в левой системе координат (рис. 7) вычисленные по формуле площади s фигуры на рис. 3 будут положительны, площади же фигур на рис. 2 и 4 — отрицательны.
О поверхности. Подобно тому, как была выше определена О (в геометрии) плоскости, может быть определена О (в геометрии) любой поверхности, делящей пространство на две части (например, сферы). Для этого рассматриваются куски поверхности, ограниченные простыми замкнутыми линиями. Ориентировать такой кусок поверхности — это значит выбрать определенную О (в геометрии) ограничивающей его кривой. Два куска поверхности называются ориентированными одинаково, если при обходе ограничивающих эти куски поверхности кривых в указанном направлении сами куски поверхности остаются с одной и той же стороны. Например, поверхности на рис. 8 и 9 двух кубов ориентированы одинаково, а поверхность третьего (рис. 10) — противоположным образом. Поверхность вместе с определенной О (в геометрии) кусков, ограниченных простыми замкнутыми кривыми, и называют ориентированной поверхностью. Не всякая поверхность может быть ориентирована (см. Ориентируемая поверхность). Однако поверхности, ограничивающие часть пространства, всегда принадлежат к числу ориентируемых.
О пространства. Пусть замкнутая поверхность ограничивает определенный кусок пространства. Говорят, что такая поверхность ориентирована правым образом, если куски этой поверхности, наблюдаемые снаружи, представляются ориентированными против часовой стрелки, подобно кубам на рис. 8 и 9. Наоборот, О (в геометрии) замкнутой поверхности, ограничивающей кусок пространства, считается левой, если ее куски ориентированы при наблюдении снаружи по часовой стрелке, подобно кубу на рис. 10. Выбор определенной О (в геометрии) замкнутых поверхностей без самопересечений называется О (в геометрии) самого трехмерного пространства. Т. о., существуют две О (в геометрии) трехмерного пространства: правая и левая. О (в геометрии) пространства можно установить также при помощи выбора системы декартовых координат. Если выбраны оси координат Ox, Оу и Oz с определенными положительными направлениями на них, то соответствующая О (в геометрии) пространства определяется следующим условием: рассматривается какой-либо тетраэдр ОАВС с вершиной О в начале и вершинами А, В, С соответственно на положительных лучах осей Ox, Оу и Oz (рис. 11, 12), треугольник АВС, лежащий на поверхности этого тетраэдра, ориентируется в порядке АВС (т. е. от оси Ox к оси Оу и затем к оси Oz); этим определяется О (в геометрии) поверхности тетраэдра, а следовательно, и всего пространства. Выбор осей на рис. 11 соответствует правой О (в геометрии) пространства, выбор же осей на рис. 12 — левой О (в геометрии) пространства. По указанному принципу сами системы координат в пространстве разделяются на правые и левые. От выбора О (в геометрии) пространства зависит знак объемов, ограниченных ориентированными поверхностями, смысл векторного произведения двух векторов и т.п.
В научной и учебной литературе употребляются как левая, так и правая системы пространственных координат. Например, в отечественных сочинениях по математике распространено употребление левой системы, в сочинениях же по механике и физике — правой системы.
Понятие "О (в геометрии)" распространяется также и на многомерные пространства.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 24.02.2026 19:40:43
|

|

|
 |
|

|
 |
 |
 |
|