
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Определитель | Определитель (далее О), детерминант, особого рода математическое выражение, встречающееся в различных областях математики. Пусть дана матрица порядка n, т. е. квадратная таблица, составленная из п2 элементов (чисел, функций и т. п.):
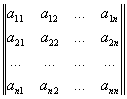 (1) (1)
(каждый элемент матрицы снабжен двумя индексами: первый указывает номер строки, второй — номер столбца, на пересечении которых находится этот элемент). Определителем матрицы (1) называется многочлен, каждый член которого является произведением n элементов матрицы (1), причем из каждой строки и каждого столбца матрицы в произведение входит лишь один сомножитель, т. е. многочлен вида
å ± a1aa2b...ang. (2)
В этой формуле a, b, ..., g есть произвольная перестановка чисел 1, 2, ..., n. Перед членом берется знак +, если перестановка a, b, ..., g четная, и знак – , если эта перестановка нечетная. (Перестановку называют четной, если в ней содержится четное число нарушений порядка (или инверсий), т. е. случаев, когда большее число стоит впереди меньшего, и нечетной – в противоположном случае; так, например, перестановка 51243 – нечетная, т. к. в ней имеется 5 инверсий 51, 52, 54, 53, 43.) Суммирование производится по всем перестановкам a, b, ..., g чисел 1, 2, ..., n. Число различных перестановок n символов равно n! = 1·2·3·...·n; поэтому О содержит n! членов, из которых 1/2n! берется со знаком + и 1/2n! со знаком –. Число n называется порядком О
О, составленный из элементов матрицы (1), записывают в виде:
 (3) (3)
(или, сокращенно, в виде |aik|). Для О 2-го и 3-го порядков имеем формулы:
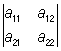 = a11a22 – a12a21, = a11a22 – a12a21,
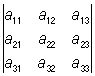 = a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31. = a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.
О 2-го и 3-го порядков допускают простое геометрическое истолкование: 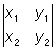 равен площади параллелограмма, построенного на векторах a1 = (x1, y1) и a2 = (х2.у2), а равен площади параллелограмма, построенного на векторах a1 = (x1, y1) и a2 = (х2.у2), а 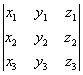 равен объему параллелепипеда, построенного на векторах a1 = (x1, y1, z1), a2 = (x2, у2, z2) и а3 = (х3, y3, z3) (системы координат предполагаются прямоугольными). равен объему параллелепипеда, построенного на векторах a1 = (x1, y1, z1), a2 = (x2, у2, z2) и а3 = (х3, y3, z3) (системы координат предполагаются прямоугольными).
Теория О возникла в связи с задачей решения систем алгебраических уравнений 1-й степени (линейные уравнения). В наиболее важном случае, когда число уравнений равно числу неизвестных, такая система может быть записана в виде:
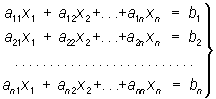 (4) (4)
Эта система имеет одно определенное решение, если О |aik|, составленный из коэффициентов при неизвестных, не равен нулю; тогда неизвестное xm (m = 1, 2, ..., n) равно дроби, у которой в знаменателе стоит О|aik|, а в числителе — О, получаемый из |aik| заменой элементов m-го столбца (т. е. коэффициентов при хт) числами b1, b2, ..., bn. Так, в случае системы двух уравнений с двумя неизвестными
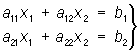
решение дается формулами
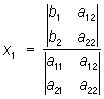 ; ; 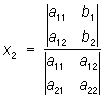 . .
Если b1 = b2 = ..., = bn = 0, то систему (4) называется однородной системой линейных уравнений. Однородная система имеет отличные от нуля решения, только если |aik| = 0. Связь теории О с теорией линейных уравнений позволила применить теорию О к решению большого числа задач аналитической геометрии. Многие формулы аналитической геометрии удобно записывать при помощи О; например, уравнение плоскости, проходящей через точки с координатами (x1, y1, z1), (x2, y2, z2), (х3, y3, z3), может быть записано в виде:
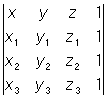 = 0. = 0.
О обладают рядом важных свойств, которые, в частности, облегчают их вычисление. Простейшие из этих свойств следующие:
1) . не изменяется, если в нем строки и столбцы поменять местами:
 = = 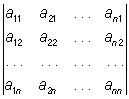 ; ;
2) О меняет знак, если в нем поменять местами две строки (или два столбца); так, например:
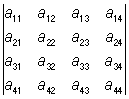 = – = –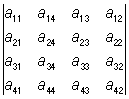 ; ;
3) О равен нулю, если в нем элементы двух строк (или двух столбцов) соответственно пропорциональны; так, например:
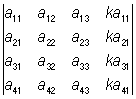 = 0; = 0;
4) общий множитель всех элементов строки (или столбца) О можно вынести за знак О; так, например:
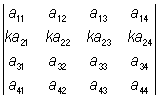 = k = k 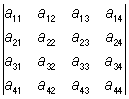 ; ;
5) если каждый элемент какого-нибудь столбца (строки) О есть сумма двух слагаемых, то О равен сумме двух О, причем в одном из них соответствующий столбец (строка) состоит из первых слагаемых, а в другом — из вторых слагаемых, остальные же столбцы (строки) — те же, что и в данном О; так, например:
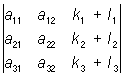 = = 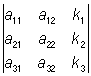 + + 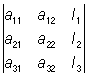 ; ;
6) О не изменяется, если к элементам одной строки (столбца) прибавить элементы другой строки (другого столбца), умноженные на произвольный множитель; так, например:
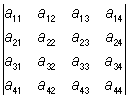 = = 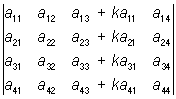 ; ;
7) О может быть разложен по элементам какой-либо строки или какого-либо столбца. Разложение О (3) по элементам i-й строки имеет следующий вид:
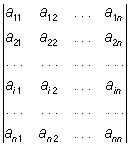 = ai1A i1 + ai2Ai2 + ...+ainAin. = ai1A i1 + ai2Ai2 + ...+ainAin.
Коэффициент Aik, стоящий при элементе aik в этом разложении, называется алгебраическим дополнением элемента aik. Алгебраическое дополнение может быть вычислено по формуле: Aik = (–1)i + kDik, где Dik — минор (подопределитель, субдетерминант), дополнительный к элементу aik, то есть О порядка n-1, получающийся из данного О посредством вычеркивания строки и столбца, на пересечении которых находится элемент aik. Например, разложение О 3-го порядка по элементам второго столбца имеет следующий вид:
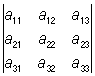 = –a12 = –a12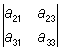 + a22 + a22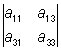 – a32 – a32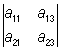 . .
Посредством разложения по элементам строки или столбца вычисление О n-го порядка приводится к вычислению n определителей (n - 1)-го порядка. Так, вычисление О 5-го порядка приводится к вычислению пяти О 4-го порядка; вычисление каждого из этих О 4-го порядка можно, в свою очередь, привести к вычислению четырех О 3-го порядка (формула для вычисления О 3-го порядка приведена выше). Однако, за исключением простейших случаев, этот метод вычисления О практически применим лишь для О сравнительно небольших порядков. Для вычисления О большого порядка разработаны различные, практически более удобные методы (для вычисления О n-го порядка приходится выполнять примерно n3 арифметических операций).
Отметим еще правило умножения двух О n-го порядка: произведение двух О n-го порядка может быть представлено в виде О того же n-го порядка, в котором элемент, принадлежащий i-й строке и k-му столбцу, получается, если каждый элемент i-й строки первого множителя умножить на соответствующий элемент k-го столбца второго множителя и все эти произведения сложить; иными словами, произведение О двух матриц равно О произведения этих матриц.
В математическом анализе О систематически используются после работ немецкого математика К. Якоби (2-я четверть 19 в.), исследовавшего О, элементы которых являются не числами, а функциями одного или нескольких переменных. Из таких О наибольший интерес представляет определитель Якоби (якобиан)
 . .
О Якоби равен коэффициенту искажения объемов при переходе от неременных х1, x2, ..., хп к переменным
y1 = f1(x1, ..., xn),
y2 = f2(x1, ..., xn),
………………….
yn = fn(x1, ..., xn).
Тождественное равенство в некоторой области этого О нулю является необходимым и достаточным условием зависимости функций f1(x1, ..., xn), f2(x1, ..., xn), ..., fn(x1, ..., xn).
Во 2-й половине 19 в. возникла теория О бесконечного порядка. Бесконечными О называются выражения вида:
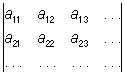 (5) (5)
(односторонний бесконечный О) и
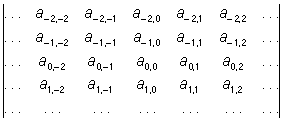
(двусторонний бесконечный О). Бесконечный О (5) есть предел, к которому стремится О

при бесконечном возрастании числа n. Если этот предел существует, то О (5) называется сходящимся, в противном случае — расходящимся. Исследование двустороннего бесконечного О иногда можно привести к исследованию некоторого одностороннего бесконечного О
Теория О конечного порядка создана в основном во 2-й половине 18 в. и 1-й половине 19 в. (работами швейцарского математика Г. Крамера, французских математиков А. Вандермонда, П. Лапласа, О Коши, немецких математиков К. Гаусса и К. Якоби). Термин "О" ("детерминант") принадлежит К. Гауссу, современное обозначение — английскому математику А. Кэли.
Лит. см. при статьях Линейная алгебра, Матрица. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 15.02.2026 14:30:11
|

|

|
 |
|

|
 |
 |
 |
|