
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Онсагера теорема | Онсагера теорема (далее О), одна из основных теорем термодинамики неравновесных процессов, установлена в 1931 Л. Онсагером. В термодинамических системах, в которых имеются градиенты температуры, концентраций компонентов, потенциалов, возникают необратимые процессы теплопроводности, диффузии, реакций. Эти процессы характеризуются тепловыми и диффузионными потоками, скоростями реакций и т.д. Они называются общим термином "потоки" и обозначаются Ji, а вызывающие их причины (отклонения термодинамических параметров от равновесных значений) — термодинамическими силами (Хк). Связь между Ji и Хк, если термодинамические силы малы, записывают в виде линейных уравнений
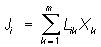 (i = 1, 2, …, m) ,(1) (i = 1, 2, …, m) ,(1)
где кинетические коэффициенты Lik определяют вклад различных термодинамических сил Хк в создание потока Ji. Соотношения (1) иногда называют феноменологическими уравнениями, a Lik — феноменологический коэффициент; значения Lik рассчитывают или находят опытным путем. Термодинамические потоки и силы могут быть скалярами (случай объемной вязкости), векторами (теплопроводность, диффузия) и тензорами (сдвиговая вязкость).
Согласно О, если нет поля и вращения системы как целого, то
Lik = Lki . (2)
В том же случае, когда на систему действует внешнее поле Н или система вращается с угловой скоростью w,
Lik () = Lki (–), Lik (w) = Lki (– w). (3)
Соотношения симметрии (2) и (3), которые иногда называют соотношениями взаимности Онсагера, устанавливают связь между кинетическим коэффициентом при т. н. перекрестных процессах (например, между коэффициентом термодиффузии и коэффициентом Дюфура эффекта, обратного термодиффузии). В отсутствие поля и вращения эти коэффициенты равны между собой, в частности равны кинетическому коэффициенту для перекрестных реакций.
Лит.: Гроот С. Р. де, Термодинамика необратимых процессов, пер. с англ., М., 1956; Денбиг К., Термодинамика стационарных необратимых процессов, пер. с англ., М., 1954; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971.
Д. Н. Зубарев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 24.02.2026 21:28:04
|

|

|
 |
|

|
 |
 |
 |
|