
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Общий интеграл | Общий интеграл (далее О) обыкновенного дифференциального уравнения
(x, у, у",..., y (n)) =0
— соотношение
(х, у, 1,..., n) =0,
содержащее и существенных произвольных постоянных 1,..., n, следствием которого является данное дифференциальное уравнение (см. Дифференциальные уравнения). Иными словами, это уравнение должно представлять собой результат исключения постоянных 1 (i = 1,..., n) из уравнений:
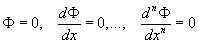 , (*) , (*)
причем эти постоянные существенны в том смысле, что процесс исключения их из системы (*) не может привести к дифференциальному уравнению, отличному от данного. О тесно связан с общим решением. Если постоянным i, входящим в О, дать определенные значения, то получим частый интеграл. Неполное исключение постоянных i из системы (*) приводит к промежуточному интегралу
k (х, у, у",..., у (n-k)), 1,..., k = 0
(где 1 £ k £ n—1); в частности, при k = 1— к первому интегралу. Геометрически О представляет n-параметрическое семейство интегральных кривых.
Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 11.03.2026 21:47:07
|

|

|
 |
|

|
 |
 |
 |
|