
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Обратные тригонометрические функции | Обратные тригонометрические функции (далее О), аркфункции, круговые функции, решают следующую задачу: найти дугу (число) по заданному значению ее тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть О: 1) Arc sin х ("арксинус x") — функция, обратная sin х; 2) Arc cos x ("арккосинус x") — функция, обратная cos х; 3) Arc tg x ("арктангенс x") — функция, обратная tg х; 4) Arc ctg x ("арккотангенс x") — функция, обратная ctg x; 5) Arc sec x ("арксеканс x") — функция, обратная sec x; 6) Arc cosec x ("арккосеканс x") — функция, обратная cosec x. Согласно этим определениям, например, х = Arc sin a есть любое решение уравнения sin х = a, т.е. sin Arc sin a = a. Функции Arc sin x и Arc cos x определены (в действительной области) для |х| £ 1, функции Arc tg х и Arc ctg х — для всех действительных х, а функции Arc sec х и Arc cosec х:—для |х| ³ 1; две последние функции малоупотребительны.
Так как тригонометрические функции периодические, то обратные к ним функции являются многозначными функциями. Определенные однозначные ветви (главные ветви) этих функций обозначаются так: arc sin х, arc cos x,..., arc cosec x. Именно, arc sin х есть та ветвь функции Arc sin х, для которой — p/2 £ arc sin х £ p/2. Аналогично, функции arc cos х, arc tg х и arc ctg х определяются из условий: 0 £ arc cos х £ p, — p/2 < arc tg x < p/2, 0 <arc ctg x < p. На рис. изображены графики функций у = Arc sin x, у = Arc cos x, у = Arc tg x, у = Arc ctg x; главные Arc cos x = ± arc cos x +2pn,ветви этих функций выделены жирной линией. О Arc sin х,... легко выражаются через arc sin x,..., например
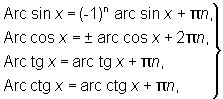 
n = 0, ±1, ±2, …
Известные соотношения между тригонометрическими функциями приводят к соотношениям между О, например из формулы
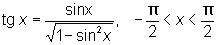
вытекает, что
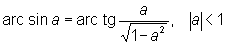
Производные О имеют вид
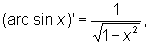
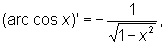
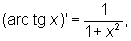
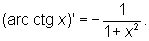
О могут быть представлены степенными рядами, например<

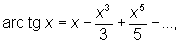
эти ряды сходятся для —1 £ x £ 1.
О можно определить для произвольных комплексных значений аргумента; однако их значения будут действительными лишь для указанных выше значений аргумента. О комплексного аргумента могут быть выражены с помощью логарифмической функции, например
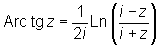 . .
Лит.: Новоселов С. И., О, 3 изд., М., 1950. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 24.02.2026 19:31:36
|

|

|
 |
|

|
 |
 |
 |
|