
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Обратные гиперболические функции | Обратные гиперболические функции (далее О), функции, обратные по отношению к гиперболическим функциям sh х, ch х, th х; они выражаются формулами
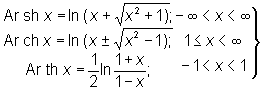 (*) (*)
(читается: ареа-синус гиперболический, ареа-косинус гиперболический, ареа-тангенс гиперболический). Эти обозначения происходят от лат. area — площадь (гиперболические функции могут рассматриваться как функции площади гиперболического сектора). Производные О имеют вид
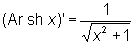 , ,
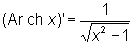 , ,
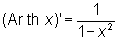 . .
Поэтому О часто появляются при интегрировании рациональных дробей и квадратичных иррациональностей.
О, рассматриваемые в комплексной области, многозначны. Их однозначные ветви (главные значения) получаются, если в формулах (*) брать для логарифма его главные значения; они обозначаются ar sh z; ar ch z, ar th z. Главные значения О связаны с главными значениями обратных тригонометрических функций формулами
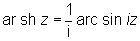 , ,
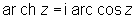 , ,
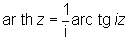 . .
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 24.02.2026 19:31:25
|

|

|
 |
|

|
 |
 |
 |
|