|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Обратная функция | Обратная функция (далее О), функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) - данная функция, то переменная х, рассматриваемая как функция переменной у, х = j (y), является обратной по отношению к данной функции у = f (x). Например, О для у = ax + b (а¹0) является х = (у-b)/a, О для у = ех является х = ln у и т.д. Если х = j(y) есть О по отношению к у = f (x), то и у = f (x) есть О по отношению к х = j(y). Областью определения О является область значений данной функции, а областью значений О- область определения данной. Графики двух взаимно обратных функций у = f (x) и у = j (x) (где независимое переменное обозначено одной и той же буквой х), как, например, у = ax + b и у = (х-b)/a, у = ех и у = ln х, симметричны по отношению к биссектрисе у = х первого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции х2 и 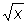 ). Для однозначности О необходимо и достаточно, чтобы данная функция у = f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). О по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.
Если данная функция кусочно монотонна, то, разбивая область ее определения на участки ее монотонности, получают однозначные ветви О Так, одним из участков монотонности для sin х служит интервал - p/2< x < p/2; ему соответствует т. н. главная ветвь arc sin х обратной функции Arc sin х. Для пары однозначных взаимно обратных функций имеют место соотношения j(f (x))=x и f (j(x)) = х, первое из которых справедливо для всех значений х из области определения функции f (x), а второе - для всех значений х из области определения функции j (x); например, elnx = х (х > 0), 1n (ex) = х (- ¥ < х < ¥). Иногда функцию, обратную к f (x) =у, обозначают f- -1(y) = х, так что для непрерывной и монотонной функции f (x):
-1(f (x))=f (f -1) x))=x.
Вообще же f --1(f (x)) представляет собой многозначную функцию от х, одним из значений которой является х; так, для f (x) = x2, х (¹ 0) является лишь одним из двух значений f --1(f (x)) = √x2 (другое: -х); для f (x) = sin х, х является лишь одним из бесконечного множества значений
f- -1(f (x)) = Arc sin (sin x) = (-1) n x + np,
n = 0, ± 1, ± 2,....
Если у = f (x) непрерывна и монотонна в окрестности точки х = x0 и дифференцируема при х = x0, причем f"(x0) ¹ 0, то f --1(y) дифференцируема при у = у0 и
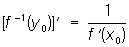
(формула дифференцирования О). Так, для -p/2 < х < p/2, у = f (x) = sin х непрерывна и монотонна, f`(x) = cos х ¹ 0 и f- -1(y)= arc sin у (-1< y <1) дифференцируема, причем
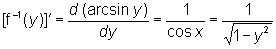
где имеется в виду положительное значение корня (так как cos х > 0 для -p/2 < х < p/2).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.12.2024 20:12:07
|
|
|
|
|
|
|
|
|
|
|
