|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Обобщенные функции | Обобщенные функции (далее О), математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие О, с одной стороны, дает возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки (пространственная), плотность простого или двойного слоя, интенсивность мгновенного источника и т.д. С другой стороны, в понятии О находит отражение тот факт, что реально нельзя измерить значение физич. величины в точке, а можно измерять лишь ее средние значения в достаточно малых окрестностях данной точки. Таким образом, О служат удобным аппаратом для описания распределений различных физических величин. Поэтому в иностранной литературе О называют распределениями.
О были введены впервые в конце 20-х гг. 20 в. П. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие дельта-функции и ее производных. Основы математической теории О были заложены С. Л. Соболевым в 1936 при решении Коши задачи для гиперболич. уравнений, а в послевоенные годы французский математик Л. Шварц дал систематическое изложение теории О В дальнейшем теорию О интенсивно развивали многие математики, главным образом в связи с потребностями математической физики. Теория О имеет многочисленные применения и все шире входит в обиход физика, математика и инженера.
Формально О определяются как линейные непрерывные функционалы над тем или иным линейным пространством основных функций j(x). Основным пространством функций является, например, совокупность бесконечно дифференцируемых финитных функций, снабженная надлежащей сходимостью (или, точнее, топологией). При этом обычные локально суммируемые функции f (x) отождествляются с функционалами (регулярными О) вида
(f, j) = òf (x)j(x) dx. (1)
Произвольная О f определяется как функционал f`, задаваемый равенством
(f¢, j) = ‑ (f, j¢). (2)
При таком соглашении каждая О бесконечно дифференцируема (в обобщенном смысле). Равенство (2) в силу (1) есть не что иное, как обобщение формулы интегрирования по частям для дифференцируемых в обычном смысле функций f (x), так что в этом случае оба понятия производной совпадают.
Сходимость на (линейном) множестве О вводится как слабая сходимость функционалов. Оказывается, что операция дифференцирования О непрерывна, а сходящаяся последовательность О допускает почленное дифференцирование бесконечное число раз.
Вводятся и другие операции над О, например свертка функций, Фурье преобразование, Лапласа преобразование. Теория этих операций приобретает наиболее простую и законченную форму в рамках понятия О, расширяющих возможности классического математического анализа. Поэтому использование О существенно расширяет круг рассматриваемых задач и к тому же приводит к значительным упрощениям, автоматизируя элементарные операции.
Примеры. 1) d-функция Дирака:
(d, j) = j(0),
описывает плотность массы (заряда) 1, сосредоточенной в точке х = 0, единичный импульс.
2) q (x) - функция Хевисайда: q(x) = 0, х £ 0, q(x) = 1, x > 0, q" = d;
производная от нее равна единичному импульсу.
3) -d" - плотность диполя момента 1 в точке х = 0, ориентированного вдоль оси х.
4) mds - плотность простого слоя на поверхности с поверхностной плотностью m:
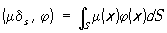
5) 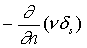 - плотность двойного слоя на поверхности с поверхностной плотностью момента n диполей, ориентированных вдоль направления нормали n:
 .
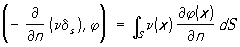6) Свертка
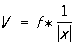
- ньютонов потенциал с плотностью f, где f - любая О (например, из 1), 3), 4) и 5)).
7) Общее решение уравнения колебаний струны
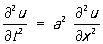
задается формулой
u (х, t) = f (x + at) + g (x - at),
где f и g - любые О
Лит.: Дирак П. А. М., Основы квантовой механики, пер. с англ., М.-Л., 1932; Soboleff ., Méthode nouvelle á resoudre le probléme de Cauchy pour les équations lineaires hyperboliques normales, "Математический сборник", 1936, т. 1 (43), № 1 (резюме на рус. яз.); Schwartz L., éorie des distributions, t. 1-2, ., 1950-51; Гельфанд И. М., Шилов Г. Е., О и действия над ними, 2 изд., М., 1959; Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971.
В. С. Владимиров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:17:13
|
|
|
|
|
|
|
|
|
|
|
