
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Нормальное распределение | Нормальное распределение (далее Н), одно из важнейших распределений вероятностей. Термин "Н" применяют как по отношению к распределениям вероятностей случайных величин, так и по отношению к совместным распределениям вероятностей нескольких случайных величин (т. е. к распредслениям случайных векторов).
Распределение вероятностей случайной величины Х называется нормальным, если оно имеет плотность вероятности
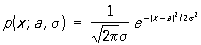 . (*) . (*)
Семейство Н (*) зависит, т. о., от двух параметров а и s. При этом математическое ожидание Х равно а, дисперсия Х равна s2. Кривая Н у = р (х; а, s) симметрична относительно ординаты, проходящей через точку х = а, и имеет в этой точке единственный максимум, равный 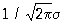 . С уменьшением s кривая Н становится все более и более островершинной (см. рис.). Изменение а при постоянном s не меняет форму кривой, а вызывает лишь ее смещение по оси абсцисс. Площадь, заключенная под кривой Н, всегда равна единице. При a = 0, s = 1 соответствуюшая функция распределения равна . С уменьшением s кривая Н становится все более и более островершинной (см. рис.). Изменение а при постоянном s не меняет форму кривой, а вызывает лишь ее смещение по оси абсцисс. Площадь, заключенная под кривой Н, всегда равна единице. При a = 0, s = 1 соответствуюшая функция распределения равна
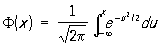 . .
В общем случае функция распределения Н (*) (х; а, s) может быть вычислена по формуле (x; а, s) = Ф (t), где t = (х — а)/s. Для функции Ф (t) (и нескольких ее производных) составлены обширные таблицы. Для Н вероятность неравенства 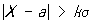 , равная 1— Ф (k)+ Ф (— k), убывает весьма быстро с ростом k (см. таблицу). , равная 1— Ф (k)+ Ф (— k), убывает весьма быстро с ростом k (см. таблицу).
k
| Вероятность< |
1
|
0,31731
|
2
|
0,04550
|
3
|
0,00269
|
4
|
0,00006
|
Во многих практических вопросах при рассмотрении Н пренебрегают поэтому возможностью отклонений от а, превышающих 3s, — т. н. правило трех сигма (соответствующая вероятность, как видно из таблицы, меньше 0,003). Вероятное отклонение для Н равно 0,67449s.
Н встречается в большом числе приложений. Издавна известны попытки объяснения этого обстоятельства. Теоретическое обоснование исключительной роли Н дают предельные теоремы теории вероятностей (см. также Лапласа теорема, Ляпунова теорема). Качественно соответствующий результат может быть объяснен следующим образом: Н служит хорошим приближением каждый раз, когда рассматриваемая случайная величина представляет собой сумму большого числа независимых случайных величин, максимальная из которых мала по сравнению со всей суммой.
Н может появляться также как точное решение некоторых задач (в рамках принятой математической модели явления). Так обстоит дело в теории случайных процессов (в одной из основных моделей броуновского движения). Классические примеры возникновения Н как точного принадлежат К. Гауссу (закон распределения ошибок наблюдения) и Дж. Максвеллу (закон распределения скоростей молекул).
Совместное распределение нескольких случайных величин X1, X2,..., Xs называется нормальным (многомерным нормальным), если соответствующая плотность вероятности имеет вид:
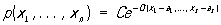 , где , где 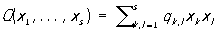 , ,
qk, l = ql, k — положительно определенная квадратичная форма. Постоянная С определяется из того условия, что интеграл от р по всему пространству равен 1. Параметры a1,..., as равны математическим ожиданиям X1,..., Xs соответственно, а коэффициент qk, l могут быть выражены через дисперсии s12,..., ss2 этих величин и коэффициент корреляции sk, l между Xk и Xl. Общее количество параметров, задающих Н, равно
(s + 1)(s + 2)/2 - 1
и быстро растет с ростом s (оно равно 2 при s = 1, 20 при s = 5 и 65 при s = 10). Многомерное Н служит основной моделью статистического анализа многомерного. Оно используется также в теории случайных процессов (где рассматривают также Н в бесконечномерных пространствах).
О вопросах, связанных с оценкой параметров Н по результатам наблюдений, см. статьи Малые выборки и Несмещенная оценка. О проверке гипотезы нормальности см. Непараметрические методы (в математической статистике).
Лит. см. при ст. Распределения.
Ю. В. Прохоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:21:31
|

|

|
 |
|

|
 |
 |
 |
|