
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Нормаль | Нормаль (далее Н) (франц. normal, от лат. normalis — прямой) к кривой (к поверхности) в данной ее точке — прямая, проходящая через эту точку и перпендикулярная к касательной прямой (касательной плоскости) в этой же точке кривой (поверхности). Плоская кривая имеет в каждой точке единственную Н, расположенную в плоскости кривой. Если х = f (t) и у = g (t) — параметрические уравнения плоской кривой L, то уравнение Н в точке (x0, y0) кривой L, соответствующей значению t0 параметра t, может быть записано в виде:
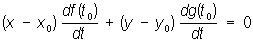 . .
Для плоской кривой, заданной уравнением (х, у) = 0, уравнение Н имеет вид:
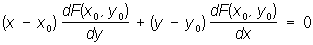 . .
Пространственная кривая имеет в каждой своей точке бесчисленное множество Н, заполняющих некоторую плоскость (нормальную плоскость). Н, лежащая в соприкасающейся плоскости, называется главной нормалью. Н, перпендикулярную к соприкасающейся плоскости, называется бинормалью. Касательная, главная Н и бинормаль образуют подвижный триэдр кривой.
Для поверхности, заданной уравнением (х, у, z) = 0, Н может быть представлена уравнениями:
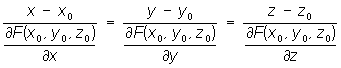 . .
Понятие Н играет существенную роль не только в дифференциальной геометрии, но и в различных ее приложениях: в геометрической оптике (например, в формулировке основных законов преломления и отражения световых лучей), в механике (материальная точка или тело при перемещениях по гладким линиям или поверхностям испытывают реакцию, направленную по Н, в консервативном поле силовые линии в каждой точке имеют направление Н к изопотенциальной поверхности, проходящей через эту точку, и т.д.).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:48:06
|

|

|
 |
|

|
 |
 |
 |
|