
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Асимптотическое выражение | Асимптотическое выражение (далее А)сравнительно простая элементарная функция, приближенно равная (с как угодно малой относительной погрешностью) более сложной функции при больших значениях аргумента (или при значениях аргумента, близких к данному значению, например нулю); Асимптотическое выражение иногда называется также асимптотической формулой или оценкой. Точное определение: функция j(x) является Асимптотическое выражение для f(x) при х ® ¥ (или х ® а), если f(x)/j(x) ® 1 при х ® ¥ (или х ® а), или, что то же самое, если f(x) = j(x)(1 + a(x)), где a(х) ® 0 при х ® ¥ (или х ® а). В этом случае пишут: f(x) ~ j(x) при х ® ¥ (или х ® а). Как правило, j(x) должна быть легко вычислимой функцией. Простейшими примерами Асимптотическое выражение при х ® 0 могут служить sinx ~ x, tgx ~ x, ctgx ~ 1/x, 1 - cosx ~ x22, ln(1 + x) ~ x, ax - 1 ~ xlna (a > 0, a ¹ 1). Более сложные Асимптотическое выражение при х ® ¥ возникают для важных функций из теории чисел и специальных функций математической физики. Например, p(x) ~ x/lnх, где p(x) — число простых чисел, не превосходящих х,
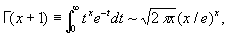
где Г(u) — гамма-функция , для целочисленных значений х = n имеем Г(n + 1) = n!, что приводит к Стирлинга формуле:
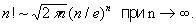
Еще более сложными Асимптотическое выражение обладают, например, Бесселя функции.
Асимптотическое выражение рассматриваются также в комплексной плоскости z = x + iy. Так, например, sin(x + iy) ~ e/y//2 при y ® ¥ и y ® -¥.
Асимптотическое выражение является, вообще говоря, частным случаем (главным членом) более сложных (и точных) приближенных выражений, называемых асимптотическими рядами, или разложениями.
Лит.: де Брейн Н. Г., Асимптотические методы в анализе, пер. с англ., М., 1961; Евграфов М. А., Асимптотические оценки и целые функции, 2 изд., М., 1962.
В. И. Левин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:43:16
|

|

|
 |
|

|
 |
 |
 |
|