
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Несмещенная оценка | Несмещенная оценка (далее Н) оценка параметра распределения вероятностей по наблюденным значениям, лишенная систематической ошибки. Более точно: если оцениваемое распределение зависит от параметров q1, q2,..., qs, то функция qi* (x1, x2,..., xn) от результатов наблюдения x1, x2,..., xn называемых Н для параметра qi, если при любых допустимых значениях параметров q1, q2,..., qs математическое ожидание Е qi* (x1, x2,..., xn) = qi,. Например, если. x1, x2,..., xn суть результаты n независимых наблюдений случайной величины, имеющей нормальное распределение
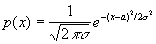
с неизвестными а (математическое ожидание) и s2 (дисперсия), то среднее арифметическое
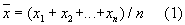
будет Н для а. Часто используемая для оценки эмпирической дисперсии
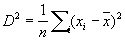
не является несмещенной оценкой. Н для s2 служит
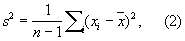
величина Н квадратичного отклонения s имеет более сложное выражение
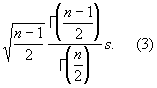
Оценка (1) для математического ожидания и оценка (2) для дисперсии являются Н и при распределениях, отличных от нормального; оценка (3) для квадратичного отклонения, вообще говоря (при распределениях, отличных от нормального), может быть смещенной.
Использование Н необходимо при оценке неизвестного параметра по большому числу серий наблюдений, каждая из которых состоит из небольшого числа наблюдений. Пусть, например, имеется k серий
xi1, xi2,×××, xin (i = 1, 2, ×××, k)
по n наблюдений в каждой и пусть si — несмещенная оценка s2 для s2, составленная по i-й серии наблюдений. Тогда при большом k в силу закона больших чисел
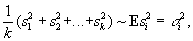
даже когда n невелико. Н играют важную роль в статистическом контроле массовой продукции.
Лит.: Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Колмогоров А. Н., Несмещенные оценки, "Изв. А. Н. СССР. Серия математическая", 1950, № 4: Гнеденко Б. В., Беляев Ю. К.. Соловьев А. Д., Математические методы в теории надежности, М., 1965.
Ю. В. Прохоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 04:48:25
|

|

|
 |
|

|
 |
 |
 |
|