
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Непараметрические методы | Непараметрические методы (далее Н)в математической статистике, методы непосредственной оценки теоретического распределения вероятностей и тех или иных его общих свойств (симметрии и т.п.) по результатам наблюдений. Название Непараметрические методы подчеркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений), и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Разработка Непараметрические методы является в значительной степени заслугой советских ученых.
В качестве примера Непараметрические методы можно привести найденный А. Н. Колмогоровым способ проверки согласованности теоретических и эмпирических распределений (так называемый критерий Колмогорова). Пусть результаты n независимых наблюдений некоторой величины имеют функцию распределения (x) и пусть n (x) обозначает эмпирическую функцию распределения (см. Вариационный ряд), построенную по этим n наблюдениям, a Dn - наибольшее по абсолютной величине значение разности n (x) - (x). Случайная величина
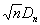
имеет в случае непрерывности (x) функцию распределения n (l), не зависящую от (x) и стремящуюся при безграничном возрастании n к пределу
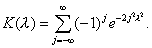
Отсюда при достаточно больших n, для вероятности pn,l. Неравенства
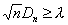
получается приближенное выражение
pn,l " 1 - К (l). (*)
Функция К (l) табулирована. Ее значения для некоторых А приведены в табл.
Таблица функции К (l)
l
|
0,57
|
0,71
|
0,83
|
1,02
|
1,36
|
1,63
|
К (l)
|
0,10
|
0,30
|
0,50
|
0,75
|
0,95
|
0,99
|
Равенство (*) следующим образом используется для проверки гипотезы о том, что наблюдаемая случайная величина имеет функцию распределения (x): сначала по результатам наблюдений находят значение величины Dn, а затем по формуле (*) вычисляют вероятность получения отклонения n от , большего или равного наблюденному. Если указанная вероятность достаточно мала, то в соответствии с общими принципами проверки статистических гипотез (см. Статистическая проверка гипотез) проверяемую гипотезу отвергают. В противном случае считают, что результаты опыта не противоречат проверяемой гипотезе. Аналогично проверяется гипотеза о том, получены ли две независимые выборки, объема n1 и n2 соответственно, из одной и той же генеральной совокупности с непрерывным законом распределения. При этом вместо формулы (*) пользуются тем, что вероятность неравенства
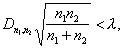
как это было установлено Н. В. Смирновым, имеет пределом К (l), здесь Dn1, n2 есть наибольшее по абсолютной величине значение разности n1 (х) - n2 (х).
Другим примером Непараметрические методы могут служить методы проверки гипотезы о том, что теоретическое распределение принадлежит к семейству нормальных распределений. Отметим здесь лишь один из этих методов - так называемый метод выпрямленной диаграммы. Этот метод основывается на следующем замечании. Если случайная величина Х имеет нормальное распределение с параметрами a и s, то
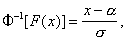
где Ф-1 - функция, обратная нормальной:
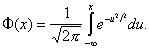
Т. о., график функции у = Ф-1( (x)) будет в этом случае прямой линией, а график функции у = Ф-1(n (x)) - ломаной линией, близкой к этой прямой (см. рис.). Степень близости и служит критерием для проверки гипотезы нормальности распределения (x).
Лит.: Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; Большее Л. Н., Смирнов Н. В., Таблицы математической статистики, М., 1968.
Ю. В. Прохоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 11.03.2026 04:21:02
|

|

|
 |
|

|
 |
 |
 |
|