Архимед

Архимед (далее А) (Archimedes; около 287 - 212 до н. э.), древнегреческий ученый, математик и механик. Развил методы нахождения площадей поверхностей и объемов различных фигур и тел. Его математические работы намного опередили свое время и были правильно оценены только в эпоху создания дифференциального и интегрального исчислений. А - пионер математической физики. Математика в его работах систематически применяется к исследованию задач естествознания и техники. А - один из создателей механики как науки. Ему принадлежат различные технические изобретения.   А родился в Сиракузах (о. Сицилия) и жил в этом городе в эпоху 1-й и 2-й Пунических войн. Предполагают, что он был сыном астронома Фидия. Научную деятельность начал как механик и техник. А совершил поездку в Египет и сблизился с александрийскими учеными, в том числе с Кононом и Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. А был близок к сиракузскому царю Гиерону . Во время 2-й Пунической войны А организовал инженерную оборону Сиракуз от римских войск. Его военные машины заставили римлян отказаться от попыток взять город штурмом и вынудили их перейти к длительной осаде. При взятии города войсками Марцелла А был убит римским солдатом, которого, по преданию, встретил словами "не трогай моих чертежей". На могиле А был поставлен памятник с изображением шара и описанного около него цилиндра. Эпитафия указывала, что объемы этих тел относятся, как 2:3 - открытие А, которое он особенно ценил.   Работы А показывают, что он был прекрасно знаком с математикой и астрономией своего времени, и поражают глубиной проникновения в существо рассматриваемых А задач. Ряд работ имеет вид посланий к друзьям и коллегам. Иногда А предварительно сообщал им без доказательств свои открытия, с тонкой иронией добавляя несколько неверных предложений.   В 9-11 вв. работы А переводились на арабский язык, с 13 в. они появляются в Зап. Европе в латинском переводе. С 16 в. начинают выходить печатные издания А, в 17-19 вв. они переводятся на новые языки. Первое издание отдельных трудов А на русском языке относится к 1823. Некоторые работы А до нас не дошли или известны лишь в отрывках, а его "Послание к Эратосфену" было найдено лишь в 1906.   Центральной темой математических работ А являются задачи на нахождение площадей поверхностей и объемов. Решение многих задач этого типа А первоначально нашел, применяя механические соображения, по существу сводящиеся к методу "неделимых" (см. "Неделимых" метод), а затем строго доказал методом исчерпывания (см. Исчерпывания метод), который он значительно развил. Рассмотрение А двусторонних оценок погрешности при проведении интеграционных процессов позволяет считать его предшественником не только И. Ньютона и Г. Лейбница, но и Г. Римана. А вычислил площадь эллипса, параболического сегмента, нашел площадь поверхности конуса и шара, объем шара и сферического сегмента, а также различных тел вращения и их сегментов. А исследовал свойства т. н. архимедовой спирали. Дал построение касательной к этой спирали, нашел площадь ее витка. Здесь он выступает как предшественник методов дифференциального исчисления. А рассмотрел также одну задачу изопериметрического типа. В ходе своих исследований он нашел сумму бесконечной геометрической прогрессии со знаменателем 1/4, что явилось первым примером появления в математике бесконечного ряда. При исследовании одной задачи, сводящейся к кубическому уравнению, А выяснил роль характеристики, которая позже получила название дискриминанта. А принадлежит формула для определения площади треугольника через 3 его стороны (неправильно именуемая формулой Герона). А дал (не вполне исчерпывающую) теорию полуправильных выпуклых многогранников (архимедовы тела). Особое значение имеет аксиома Аа (см. Аа аксиома): из неравных отрезков меньший, будучи повторен достаточное число раз, превзойдет больший. Эта аксиома определяет т. н. архимедовскую упорядоченность, которая играет важную роль в современной математике. А построил счисление, позволяющее записывать и называть весьма большие числа. 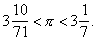Он с большой точностью вычислил значение числа p и указал пределы погрешности:   Механика постоянно находилась в круге интересов А В одной из своих первых работ он исследует распределение нагрузок между опорами балки. А принадлежит определение понятия центра тяжести тела. Применяя, в частности, интеграционные методы, он нашел положение центра тяжести различных фигур и тел. А дал математический вывод законов рычага. Ему приписывают гордую фразу: "Дай мне, где стать, и я сдвину Землю". А заложил основы гидростатики. Он сформулировал основные положения этой дисциплины, в том числе знаменитый закон А (см. Аа закон). Последняя работа А посвящена исследованию равновесия плавающих тел. При этом он выделяет устойчивые положения равновесия. А изобрел водоподъемный механизм, т. н. архимедов винт (см. Водоподъемная машина), который явился прообразом корабельных, а также воздушных винтов. Рассказывают, что А нашел решение задачи об определении количества и в жертвенной короне Гиерона, когда садился в ванну, и нагим побежал домой с криком "эврика!" ("нашел!"). А занимался также астрономией. Он сконструировал прибор для определения видимого (углового) диаметра Солнца и нашел значение этого угла с поразительной точностью. При этом А вводил поправку на размер зрачка. Он первым стал приводить наблюдения к центру Земли. Наконец, А построил небесную сферу - механический прибор, на котором можно было наблюдать движения планет, фазы Луны, солнечные и лунные затмения.   Соч.: Archimedis opera omnia cum commentariis Eutocii, ed. J. L. Heiberg, v. 1-3, Lipsiae, 1910-15; в рус. пер. - Сочинения, М., 1962 (библ. с. 635-37).   Лит.: Чвалина А, А, пер. с нем., М.-Л., 1934; Лурье С. Я., А, М.-Л., 1945; Каган В. Ф., А. Краткий очерк о жизни и творчестве, М.-Л., 1949; Веселовский И. Н., А, М., 1957; Heath Т. L., Archimedes, L., 1920.   С. Б. Стечкин.