
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Наилучшее приближение | Наилучшее приближение (далее Н) важное понятие теории приближения функций. Пусть f (x) - произвольная непрерывная функция, заданная на некотором отрезке (а, b), a j1(x), j2(x),..., jn (x) - фиксированная система непрерывных функций на том же отрезке. Тогда максимум выражения:
|f (x) - a1j1(x) - a2j2(x) -... - anjn (x)| (*)
на отрезке (а, b) называется уклонением функции f (x) от полинома
n (x) = a1j1(x) + a2j2(x) +... + anjn (x),
а минимум уклонения для всевозможных полиномов n (x) (т. е. при всевозможных наборах коэффициентов a1, a2,..., an) - наилучшим приближением функции f (x) посредством системы j1(x), j2(x),..., jn (x); Н обозначают через En (f, j). Таким образом, Н является минимумом максимума или, как говорят, минимаксом.
Полином *n (x, f), для которого уклонение от функции f (x) равно Н (такой полином всегда существует), называется полиномом, наименее уклоняющимся от функции f (x) (на отрезке (а, b)).
Понятия Н и полинома, наименее уклоняющегося от функции f (x), были впервые введены П. Л. Чебышевым (1854) в связи с исследованиями по теории механизмов. Можно также рассматривать Н, когда под уклонением функции f (x) от полинома n (x) понимается не максимум выражения (*), а, например,
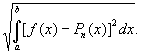
См. Приближение и интерполирование функций.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:45:44
|

|

|
 |
|

|
 |
 |
 |
|