
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Навье - Стокса уравнения | Навье — Стокса уравнения (далее Н) дифференциальные уравнения движения вязкой жидкости (газа). Названы по имени Л. Навье и Дж. Стокса. Для несжимаемой (плотность r = const) и ненагреваемой (температура Т = const) жидкости Н. — С. у. в проекциях на оси прямоугольной декартовой системы координат (система трех уравнений) имеют вид:
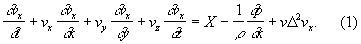
Здесь t — время, x, у, z — координаты жидкой частицы, vx, vy, vz — проекции ее скорости, X, , Z — проекции объемной силы, p — давление, v = m/r — кинематический коэффициент вязкости (m — динамический коэффициент вязкости),
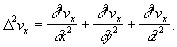
Два других уравнения получаются заменой x на у, у на z и z на x. Н. — С. у. служат для определения vx, vy, vz, р как функций x, у, z, t. Чтобы замкнуть систему, к уравнениям (1) присоединяют уравнение неразрывности, имеющее для несжимаемой жидкости вид:
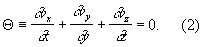
Для интегрирования уравнений (1), (2) требуется задать начальные (если движение не является стационарным) и граничные условия, которыми для вязкой жидкости являются условия прилипания к твердым стендам. В общем случае (движение сжимаемой и нагреваемой жидкости) в Н. — С. у. учитывается еще переменность r и зависимость m от температуры, что изменяет вид уравнений. При этом дополнительно используются уравнение баланса энергии и Клапейрона уравнение.
Н. — С. у. применяют при изучении движений реальных жидкостей и газов, причем в большинстве конкретных задач ограничиваются отысканием тех или иных приближенных решений.
Лит. см. при ст. Гидроаэромеханика.
С. М. Тарг.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:07:18
|

|

|
 |
|

|
 |
 |
 |
|