
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Наблюдений обработка | Наблюдений обработка (далее Н) математическая, применение к результатам наблюдений математических методов для построения выводов об истинных значениях искомых величин. Всякий результат наблюдений, связанных с измерениями, содержит ошибки (погрешности) различного происхождения. По своему характеру ошибки делятся на три группы: грубые, систематические и случайные (о грубых ошибках см. ст. Ошибок теория; в дальнейшем будет предполагаться, что наблюдения не содержат грубых ошибок). Обычно результат измерения некоторой величины m считают случайной величиной; тогда ошибка измерения d = - m будет также случайной величиной. Пусть b = Еd - математическое ожидание ошибки. Тогда = m + b + (d - b). Величину b называют систематической ошибкой, а d - b — случайной ошибкой; математическое ожидание d - b равно нулю. Систематическая ошибка b часто бывает известна заранее и в этом случае легко устраняется. Например, в астрономии при измерении величины угла между направлением на светило и плоскостью горизонта систематическая ошибка является суммой двух ошибок: систематические ошибки, которую дает прибор при отсчете данного угла (см. Инструментальные ошибки), и систематические ошибки, обусловленной преломлением лучей света в атмосфере (см. Рефракция). Инструментальная ошибка определяется с помощью таблицы или графика поправок для данного прибора; ошибку, связанную с рефракцией (для зенитных расстояний, меньших 80°), достаточно точно можно вычислить теоретически.
Влияние случайных ошибок оценивается с помощью методов теории ошибок. Если 1, 2,..., n — результаты n независимых измерений величины m, произведенных в одинаковых условиях и одинаковыми средствами, то обычно полагают
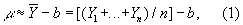
где b — систематическая ошибка. Об оценке абсолютной погрешности приближенного равенства (1) см. в статьях Наименьших квадратов метод, Значимости уровень.
В том случае, когда требуется вычислить значение некоторой функции f (y) в точке y = m, причем величина m оценивается по n независимым наблюдениям 1, 2,..., n, приближенно полагают
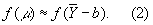
Пусть В — математическое ожидание величины
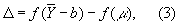
т. е.
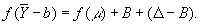
Поэтому В — систематическая ошибка и (D - В) — случайная ошибка приближенного равенства (2). Если случайные ошибки независимых наблюдений 1, 2,..., n подчиняются одному и тому же распределению и функция f (y) в окрестности точки у = m. мало отличается от линейной, то В " 0 и
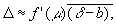
где
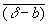
— арифметическое среднее случайных ошибок исходных наблюдений. Это означает, что если Е (di - b)2 = s2, i = 1, 2,..., n, то Е (D — В)2 " ЕD2 " (f` (m))2s2/n ® 0 при n ® ¥.
В случае нескольких неизвестных параметров Н часто осуществляется с помощью метода наименьших квадратов.
Если изучается зависимость между случайными величинами Х и на основе совокупности n независимых наблюдений, каждое из которых есть вектор (Xi, i), i = 1,..., n, компоненты которого Xi и i подчиняются исследуемому совместному распределению величин Х и , то соответствующая Н выполняется с помощью теории корреляции и математической статистики.
При Н приходится делать некоторые предположения и допущения о характере функциональной зависимости, о распределении случайных ошибок и т.д., поэтому Н должна включать в себя проверку согласия сделанных допущений с результатами использованных и др. наблюдений. См. Статистическая проверка гипотез.
Лит.: Уиттекер Э. Т. и Робинсон Г., Математическая обработка результатов наблюдений, пер. с англ., Л. — М., 1935; Линник Ю. В., Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962.
Л. Н. Большев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:06:19
|

|

|
 |
|

|
 |
 |
 |
|