
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Момент инерции | Момент инерции (далее М) величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М осевые и центробежные. Осевым М тела относительно оси z называется величина, определяемая равенством:
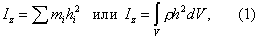
где mi — массы точек тела, hi — их расстояния от оси z, r — массовая плотность, — объем тела. Величина z является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой М можно также выразить через линейную величину k, называемую радиусом инерции, по формуле z = Mk2, где М — масса тела. Размерность М — L2M; единицы измерения — кг×м2 или г×см2.
Центробежным М относительно системы прямоугольных осей х, у, z, проведенных в точке О, называют величины, определяемые равенствами:
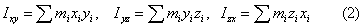
или же соответствующими объемными интегралами. Эти величины являются характеристиками динамической неуравновешенности масс. Например, при вращении тела вокруг оси z от значений xz и yz зависят силы давления на подшипники, в которых закреплена ось.
М относительно параллельных осей z и z" связаны соотношением
z = z" + М d2 (3)
где z" — ось, проходящая через центр масс тела, a d — расстояние между осями (теорема Гюйгенса).
М относительно любой, проходящей через начало координат О оси Ol с направляющими косинусами a, b, g находится по формуле:
lol = x a2 + y b2 + z g2 — 2xy ab — 2yz bg — 2zxga. (4)
Зная шесть величин x, y, z, xy, yх, zx, можно последовательно, используя формулы (4) и (3), вычислить всю совокупность М тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно-перпендикулярные оси, называемые главными осями инерции, для которых xy = yz = zx = 0. Тогда М тела относительно любой оси можно определить, зная главные оси инерции и М относительно этих осей.
М тел сложной конфигурации обычно определяют экспериментально. Понятием о М широко пользуются при решении многих задач механики и техники.
Лит.: Краткий физико-технический справочник, под общ. ред. К. П. Яковлева, т. 2, М., 1960, с. 94—101; Фаворин М. В., Моменты инерции тел. Справочник, М., 1970; Гернет М. М., Ратобыльский В. Ф., Определение моментов инерции, М., 1969; см. также лит. при ст. Механика.
С. М. Тарг.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 02.03.2026 00:44:32
|

|

|
 |
|

|
 |
 |
 |
|