
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Магнитная гидродинамика | гидродинамика (далее М)(МГД), наука о движении электропроводящих жидкостей и газов в присутствии магнитного поля; раздел физики, развившийся "на стыке" гидродинамики и классической электродинамики. Характерными для гидродинамика объектами являются плазма (настолько, что гидродинамика иногда рассматривают как раздел физики плазмы), жидкие металлы и электролиты.
Первые исследования по гидродинамика восходят ко временам М. Фарадея, но как самостоятельная отрасль знания гидродинамика стала развиваться в 20 веке в связи с потребностями астрофизики и геофизики. Было установлено, что многие космические объекты обладают полями. Так, в атмосферах звезд наблюдаются поля напряженностью ~ 10000 э (на Солнце до 5000 э), а в открытых в 1969 пульсарах, по современным представлениям, напряженности полей достигают 1012 э. Динамическое поведение находящейся в подобных полях плазмы радикально изменяется, так как плотность энергии поля становится сравнимой с плотностью кинетической энергии частиц плазмы (или превышает ее). Этот же критерий справедлив и для слабых космических полей напряженностью 10-3-10-5 э (в межзвездном пространстве, поле Земли в верхней атмосфере и за ее пределами), если в областях, занимаемых ими, концентрация заряженных частиц низка. Таким образом, возникла необходимость в создании специальной теории движения космической плазмы в полях, получившей название космической электродинамики, а в случае, когда плазму можно рассматривать как сплошную среду - космической магнитогидродинамики (космической МГД).
Основные положения гидродинамика были сформулированы в 1940-х годах Х. Альфвеном, который в 1970 за создание гидродинамика был удостоен Нобелевской премии по физике. Им было теоретически предсказано существование специфических волновых движений проводящей среды в поле, получивших название волн Альфвена. Начав формироваться как наука о поведении космической плазмы, гидродинамика вскоре распространила свои методы и на проводящие среды в земных условиях (главным образом создаваемые в научных исследованиях и в производственной деятельности). В начале 1950-х годов развитию гидродинамика, как и физики плазмы в целом, дали мощный импульс национальные программы (СССР, США, Великобритания) исследований по проблеме управляемого термоядерного синтеза. Появились и быстро совершенствуются многочисленные технические применения гидродинамика (МГД-насосы, генераторы, сепараторы, ускорители, перспективные для космических полетов плазменные двигатели и пр.).
В основе гидродинамика лежат две группы законов физики: уравнения гидродинамики и уравнения электромагнитного поля (Максвелла уравнения). Первые описывают течения проводящей среды (жидкости или газа); однако, в отличие от обычной гидродинамики, эти течения связаны с распределенными по объему среды электрическими токами. Присутствие поля приводит к появлению в уравнениях дополнительного члена, соответствующего действующей на эти токи распределенной по объему электродинамической силе (см. Ампера закон, Лоренца сила). Сами же токи в среде и вызываемые ими искажения поля определяются второй группой уравнений. Таким образом, в гидродинамика уравнения гидродинамики и электродинамики оказываются существенно взаимосвязанными. Следует отметить, что в гидродинамика в уравнениях Максвелла почти всегда можно пренебречь токами смещения (нерелятивистская гидродинамика).
В общем случае уравнения гидродинамика нелинейны и весьма сложны для решения, но в практических задачах часто можно ограничиться теми или иными предельными режимами, при оценке которых важным параметром служит безразмерная величина, называемая Рейнольдса числом:
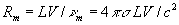 (1) (1)
(L - характерный для течения среды размер, - характерная скорость течения, nm = c2/4ps - так называемая вязкость, описывающая диссипацию энергии поля, s - электрическая проводимость среды, с - скорость света в вакууме; здесь и ниже используется абсолютная система единиц Гаусса, см. СГС система единиц).
При Rm << 1 (что обычно для лабораторных условий и технических применений) течение проводящей среды слабо искажает поле, которое поэтому можно считать заданным внешними источниками. Такое течение может быть использовано, например, для генерации электрического тока - энергия гидродинамического движения среды превращается в энергию тока во внешней цепи (см. Магнитогидродинамический генератор). Напротив, если ток в среде поддерживается внешней эдс, то наличие внешнего поля вызывает появление упомянутой выше объемной электродинамической силы, которая создает в среде перепад давления и приводит ее в движение. Этот эффект используется в МГД-насосах (например, для перекачивания расплавленного металла) и плазменных ускорителях. Объемная электродинамическая сила дает также возможность создавать регулируемую выталкивающую (архимедову) силу, которая действует на помещенные в проводящую жидкость тела. На этом важном эффекте основано действие МГД-сепараторов. Таковы основные технические применения гидродинамика Кроме того, в гидродинамика находят естественное обобщение известные задачи обычных гидродинамики и газовой динамики: обтекание тел, пограничный слой и другие; в ряде случаев (например, при полетах в ионосфере космических аппаратов, в каналах, по которым текут проводящие среды) оказывается возможным с помощью поля существенно влиять на свойства соответствующих течений.
Однако наиболее интересные и разнообразные эффекты характерны для другого предельного класса сред, рассматриваемых в гидродинамика, - для сред с Rm >> 1, то есть с высокой проводимостью и (или) большими размерами. Эти условия, как правило, выполняются в средах, изучаемых в гео- и астрофизических приложениях гидродинамика, а также в горячей (например, термоядерной) плазме. Течения в таких средах чрезвычайно сильно влияют на поле в них. Одним из важнейших эффектов в этих условиях является вмороженность поля. В хорошо (строго говоря - идеально) проводящей среде индукция электромагнитная вызывает появление токов, препятствующих какому бы то ни было изменению магнитного потока через всякий материальный контур. В движущейся МГД-среде с Rm >> 1 это справедливо для любого контура, образуемого ее частицами. В результате поток через любой движущийся и меняющий свои размеры элемент среды остается неизменным (с тем большей степенью точности, чем больше величина Rm), и в этом смысле говорят о "вмороженности" поля. Это во многих случаях позволяет, не прибегая к громоздким расчетам, с помощью простых представлений получить качественную картину течений среды и деформаций поля - следует только рассматривать силовые линии как упругие нити, на которые нанизаны частицы среды. Более строгое рассмотрение этого "упругого" действия поля на проводящую среду показывает, что оно сводится к изотропному (то есть одинаковому по всем направлениям) "магнитному" давлению рМ = 2 / 8p, которое добавляется к обычному газодинамическому давлению среды р, и натяжению Т = 2 / 4p, направленному вдоль силовых линий поля (магнитная проницаемость всех представляющих интерес для гидродинамика сред с большой точностью равна 1, и можно с равным правом пользоваться как магнитной индукцией В, так и напряженностью Н).
Наличие дополнительных "упругих" натяжений в МГД-средах приводит к специфическому колебательному (волновому) процессу - волнам Альфвена. Они обусловлены натяжением Т и распространяются вдоль силовых линий (подобно волнам, бегущим вдоль упругой нити) со скоростью
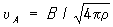 , (2) , (2)
где r - плотность среды. Волны Альфвена описываются точным решением нелинейных уравнений гидродинамика для несжимаемой среды. Ввиду сложности этих уравнений таких точных решений для больших Rm получено очень немного. Еще одно из них описывает течение несжимаемой (r = const) жидкости с той же альфвеновской скоростью (2) вдоль произвольного поля. Известно точное решение и для так называемых МГД-разрывов, которые включают контактные, тангенциальные и вращательные разрывы, а также быструю и медленную ударные волны. В контактном разрыве поле пересекает границу раздела двух различных сред, препятствуя их относительному движению (в приграничном слое среды неподвижны одна относительно другой). В тангенциальном разрыве поле не пересекает границу раздела двух сред (его составляющая, нормальная к границе, равна нулю), и эти среды могут находиться в относительном движении. Частным случаем тангенциального разрыва является нейтральный токовый слой, разделяющий равные по величине и противоположно направленные поля. В гидродинамика доказывается, что при некоторых условиях поле стабилизирует тангенциальный разрыв скорости, который абсолютно неустойчив в обычной гидродинамике. Специфическим для гидродинамика (не имеющим аналога в гидродинамике непроводящих сред) является вращательный разрыв, в котором вектор индукции, не изменяясь по абсолютной величине, поворачивается вокруг нормали к поверхности разрыва. натяжения в этом случае приводят среду в движение таким образом, что вращательный разрыв распространяется по направлению нормали к поверхности с альфвеновской скоростью (2), если под В в (2) понимать нормальную составляющую индукции. Быстрые и медленные ударные волны в гидродинамика отличаются от обычных ударных волн тем, что частицы среды после прохождения фронта волны получают касательный к фронту импульс за счет натяжений (ведь силовые линии можно рассматривать как упругие нити, см. выше). В быстрой ударной волне поле за ее фронтом усиливается, скачок давления на фронте действует в ту же сторону, что и скачок газодинамического давления, и поэтому скорость такой волны больше скорости звука в среде. В медленной ударной волне, напротив, поле после ее прохождения ослабевает, перепады газодинамического и давления на фронте волны направлены противоположно; скорость медленной волны меньше скорости звука. Число теоретически мыслимых необратимых ударных волн в гидродинамика оказывается значительно больше, чем реально существующих. Отбор решений, соответствующих действительности, производится с помощью так называемого условия эволюционности, следующего из рассмотрения устойчивости ударных волн при их взаимодействии с колебаниями малой амплитуды.
Известные точные решения, однако, далеко не исчерпывают содержания теоретических гидродинамика сред с Rm >> 1. Широкий класс задач удается исследовать приближенно. При таком исследовании возможны два основных подхода: приближение слабого поля, когда давление и натяжение малы по сравнению с остальными динамическими факторами (газодинамическим давлением и инерциальными силами), и приближение сильного поля, когда
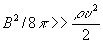 , , 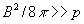 (3) (3)
здесь u - скорость среды, р - ее газодинамическое давление.
В приближении слабого поля течение среды определяется обычными газодинамическими факторами (влиянием натяжений пренебрегают). При этом требуется рассчитать изменения поля в среде, движущейся по заданному закону. К этому классу задач относится очень важная проблема гидромагнитного динамо и проблема МГД-турбулентности. Первая состоит в отыскании ламинарных течений проводящих сред, которые могут создавать, усиливать и поддерживать поле. Задача о гидромагнитном динамо является основой теории земного магнетизма и магнетизма Солнца и звезд. Существуют простые кинематические модели, показывающие, что гидромагнитное динамо в принципе может быть осуществлено при специальном выборе распределений скоростей среды. Однако строгого доказательства, что такие распределения реализуются в действительности, пока нет.
Основным в проблеме МГД-турбулентности является выяснение поведения слабого исходного ("затравочного") поля в турбулентной проводящей среде (см. Турбулентность). Имеется доказательство роста среднего квадрата напряженности случайно возникшего слабого начального поля, то есть возрастания энергии в начальной стадии процесса. Однако остается открытой проблема установившегося турбулентного состояния, связанная с происхождением полей в космическом пространстве, в частности в нашей и других галактиках.
Приближение сильного поля, в котором определяющими являются натяжения, применяют при изучении разреженных атмосфер космических тел, например Солнца и Земли. Есть основания полагать, что именно это приближение окажется полезным для исследования процессов в удаленных астрофизических объектах - сверхновых звездах, пульсарах, квазарах и прочих. В условиях, отвечающих (3), изменения поля вблизи его источников (появление активных областей и пятен на Солнце, смещение в поле Земли под действием солнечного ветра и т.д.) переносятся с альфвеновской скоростью (2) вдоль поля, вызывая соответствующие перемещения плазмы. В результате действия сил возникают такие характерные образования, как выбросы и протуберанцы, шлемовидные структуры и стримеры на Солнце, хвост Земли (см. Солнце; Солнечная активность; Земля, раздел
Особенно интересные явления имеют место в окрестностях тех точек сильного поля, в котором оно обращается в нуль. В таких областях образуются тонкие токовые слои, разделяющие поля противоположного направления (так называемые нейтральные слои). В этих слоях происходит процесс "аннигиляции" энергии, то есть ее высвобождение и превращение в другие формы. В частности, в них возникают сильные электрические поля, ускоряющие заряженные частицы. Аннигиляция поля в нейтральных токовых слоях ответственна за появление вспышек на Солнце и суббурь в земной (см. Магнитные бури). Вероятно, с ней связаны и многие другие резко нестационарные процессы во Вселенной, сопровождающиеся генерацией ускоренных заряженных частиц и жестких излучений. С точки зрения гидродинамика нейтральные слои представляют собой разрывы непрерывности поля (подобно ударным волнам и тангенциальным разрывам). Однако, процессы в токовых слоях , и прежде всего неустойчивости, приводящие к появлению сильных ускоряющих электрических полей, выходят за рамки гидродинамика и относятся к тонким и еще не вполне разработанным вопросам физики плазмы.
Лит.: Апьфвен Г., Фельтхаммар К.-Г., Космическая электродинамика, перевод с английского, 2 изд., М., 1967; Сыроватский С. И., гидродинамика, "Успехи физических наук", 1957, т. 62, в. 3; Куликовский А. Г., Любимов Г. А., гидродинамика, М., 1962; Шерклиф Дж.. Курс гидродинамики, перевод с английского, М., 1967; Половин Р. В., Ударные волны в гидродинамике, "Успехи физических наук",1960, т. 72, в. 1; Брагинский С. И., Явления переноса в плазме, в сборнике: Вопросы теории плазмы, вып. 1, М., 1963; Пикельнер С. Б., Основы космической электродинамики, М., 1966; Данжи Дж., Космическая электродинамика, перевод с английского, М., 1961; Андерсон Э., Ударные волны в гидродинамике, перевод с английского, М., 1968; Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред, М., 1959 (Теоретическая физика).
С. И. Сыроватский. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:40:37
|

|

|
 |
|

|
 |
 |
 |
|