
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Ляпунова теорема | Ляпунова теорема (далее Л) в теории вероятностей, теорема, устанавливающая некоторые весьма общие достаточные условия для сходимости распределения сумм независимых случайных величин к нормальному закону. Сформулирована и доказана А. М. Ляпуновым в 1901. Л завершает исследования П. Л. Чебышева, А. А. Маркова (старшего) и самого А. М. Ляпунова в этом основном для всей теории вероятностей направлении. Точная формулировка Л такова: пусть независимые случайные величины Xi,..., Xn, ... имеют конечные математические ожидания EXk, дисперсии DXk и при d > 0 абсолютные моменты 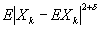 и пусть и пусть 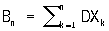 — дисперсия суммы Xi,..., Xn. Утверждается, что, если при некотором d>0 — дисперсия суммы Xi,..., Xn. Утверждается, что, если при некотором d>0
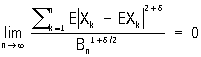
(условие Ляпунова), то вероятность неравенства
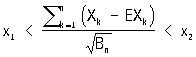
стремится при n ® ¥ к пределу
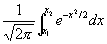
равномерно относительно всех значений x1 и x2. Ляпунов дал также оценку скорости сходимости в Л В дальнейшем были установлены условия, расширяющие условие Ляпунова и являющиеся не только достаточными, но в некотором смысле необходимыми. См. Предельные теоремы теории вероятностей.
Лит.: Ляпунов А. М., Новая форма теоремы о пределе вероятности, Собрание сочинений, т. 1, М., 1954, с. 157; Бернштейн С. Н., Теория вероятностей, 4 изд., М. — Л., 1946, с. 275.
А. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:14:16
|

|

|
 |
|

|
 |
 |
 |
|