|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Логический закон | Логический закон (далее Л), общее название законов, образующих основу логической дедукции. Понятие о Л восходит к древнегреческому понятию о lógos"e как предпосылке объективной ("природной") правильности рассуждений. Собственно логическое содержание оно впервые получает у Аристотеля, положившего начало систематическому описанию и каталогизации таких схем логических связей произвольных элементарных высказываний в сложные высказывания, убедительность (общезначимость) которых вытекает из одной только их формы, а точнее — из одного только правильного понимания смысла логических связей, безотносительно к истинностному значению элементарных высказываний. Большинство Л, открытых Аристотелем, это — законы силлогизма. Позже были открыты и другие законы и даже установлено, что множество Л бесконечно. В некотором смысле обозреть это бесконечное множество Л стало возможным благодаря различного типа формальным теориям логического рассуждения — т. н. логическим формализмам, или логическим исчислениям, в которых Л выражаются определенного вида формулами и определяются — каждый по отношению к "своему" исчислению — выводимыми формулами данного вида (т. н. "общезначимыми формулами", или теоремами исчислений, см. Логика). Существующее многообразие логических исчислений естественно порождает идею относительности Л Однако типом логического исчисления полагаются одновременно и границы этой относительности, поскольку тип исчисления не является исключительно делом произвольного выбора, а диктуется (или подсказывается) "логикой вещей", о которых хотят рассуждать, а также, в известном смысле, субъективной уверенностью в том или ином характере этой логики. Все исчисления, основанные на одной и той же гипотезе о характере "логики вещей", являются эквивалентными в том смысле, что они описывают ("порождают") одни и те же Л К примеру, исчисления, основанные на двузначности принципе, т. н. исчисления классической логики, несмотря на все их "внешнее" разнообразие, описывают один и тот же "мир" классический Л — тождественных истин, которые издавна получили общепринятую онтологическую философскую характеристику "вечных истин", или "истин во всех возможных мирах". Л интуиционистской логики никакой общепринятой онтологической интерпретации пока не получили. "Логикой вещей", отражением которой они исторически явились, была логика умственных математических построений — логика "знания", а не логика "бытия".
Изучение Л образует естественный исходный пункт логического анализа приемлемых ("хороших") способов рассуждений (умозаключений), поскольку само понятие "приемлемое, или логически правильное, рассуждение" уточняется через понятие "Л". Связь логически правильных рассуждений с Л выражается в логике т. н. теоремой о дедукции, фиксирующей ту, замеченную еще стоиками, особую роль, которую Л играют при обосновании или проверке наших умозаключений: относительно любого утверждения о выводимости заключения В из посылок А1, А2, ..., An вопрос о его истинности решается разысканием среди Л высказывания A1É(A2É)(... É(AnÉ)..*(, где É выражает логический союз "если..., то...". Указанная связь Л с умозаключениями имеет общенаучное значение и выходит далеко за пределы собственно логики, обеспечивая общий метод формального доказательства средствами логики (см. Аксиоматический метод).
М. М. Новоселов.
Термин "Л" применялся в традиционной логике по отношению к т. н. "законам мышления": закону тождества ("всякая сущность совпадает сама с собой"), закону противоречия ("никакое суждение не может одновременно быть истинным и ложным"), закону исключенного третьего ("для произвольного высказывания либо оно само, либо его отрицание истинно") и закону достаточного основания ("всякое принимаемое суждение должно быть надлежащим образом обосновано"). Первый из перечисленных принципов (термин "закон" здесь вообще представляется неуместным) есть важная предпосылка рассуждений, относящаяся, однако, не к логике, а к онтологии и к теории познания и к тому же применимая всякий раз в точно оговоренных пределах; последний принцип также не относится к логике, а имеет отчетливо выраженный методологический характер. Исключенного третьего принцип действительно принадлежит логике, но не во всякой логической системе соответствующая формула (А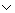 ù А) общезначима (см. Математический интуиционизм, Конструктивное направление в математике и логике). И лишь принцип противоречия (в современной логической символике: ù (А&ù А) представляет собой утверждение, не только доказуемое в любой логической системе, но и лежащее в некотором смысле в основе всей современной формальной логики.
Ю. А. Гастев.
Лит. см. при ст. Логика. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.12.2024 14:35:24
|
|
|
|
|
|
|
|
|
|
|
