
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Логические операции | Логические операции (далее Л), логические связки, логические операторы, функции, преобразующие высказывания или пропозициональные формы (т. е. выражения логики предикатов, содержащие переменные и обращающиеся в высказывания при замене последних какими-либо конкретными их значениями) в высказывания или пропозициональные формы. Л можно разделить на две основные группы: кванторы и пропозициональные (сентенциональные) связки. Кванторы играют для формализованных языков математической логики ту же роль, которую играют для естественного языка т. н. "количественные" ("кванторные") слова: "все", "любой", "некоторый", "существует", "единственный", "не более (менее) чем", количественные числительные и т. п. Характерной особенностью кванторов является - в случае нефиктивного их применения - понижение числа свободных переменных в преобразуемом выражении: применение квантора к выражению, содержащему n свободных переменных, приводит, вообще говоря, к выражению, содержащему n - 1 свободную переменную, в частности, пропозициональную форму с одной свободной переменной применение квантора (по этой переменной) преобразует в высказывание.
Пропозициональные связки (в отличие от кванторов, введение которых знаменует переход к логике предикатов) употребляются уже в самой элементарной части логики - в логике высказываний. В формализованных логических и логико-математических языках они выполняют функции, вполне аналогичные функциям союзов и союзных слов, употребляемых для образования сложных предложений в естественных языках. Так, отрицание ù истолковывается как частица "не", конъюнкция & истолковывается как союз "и", дизъюнкция 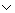 - как (неразделительное) "или", импликация É - как оборот "если..., то...", эквиваленция ~ - как оборот "тогда и только тогда, когда" и т. п. При этом, однако, соответствие между Л и средствами естественного языка отнюдь не взаимно однозначно. Во-первых, потому, что высказывания, по определению, могут принимать лишь два "истинностных значения": "истину" ("и") и "ложь" ("л"), так что пропозициональные Л можно рассматривать как различные функции, отображающие некоторую область из двух элементов в себя; поэтому число различных n-местных (т. е. от n аргументов) Л определяется из чисто комбинаторных соображений - оно равно 2n. Во-вторых, в формализованных языках математической логики игнорируются любые смысловые (и тем более стилистические) оттенки значений союзов, кроме тех, что непосредственно определяют истинностное значение получающегося сложного предложения. В свою очередь, в качестве Л рассматриваются подчас и такие связки, содержательные аналоги которых в обычном языке, как правило, не имеют специальных наименований; таков, например, "штрих Шеффера" ½ в нижеследующей таблице, где приведен полный перечень всех - как (неразделительное) "или", импликация É - как оборот "если..., то...", эквиваленция ~ - как оборот "тогда и только тогда, когда" и т. п. При этом, однако, соответствие между Л и средствами естественного языка отнюдь не взаимно однозначно. Во-первых, потому, что высказывания, по определению, могут принимать лишь два "истинностных значения": "истину" ("и") и "ложь" ("л"), так что пропозициональные Л можно рассматривать как различные функции, отображающие некоторую область из двух элементов в себя; поэтому число различных n-местных (т. е. от n аргументов) Л определяется из чисто комбинаторных соображений - оно равно 2n. Во-вторых, в формализованных языках математической логики игнорируются любые смысловые (и тем более стилистические) оттенки значений союзов, кроме тех, что непосредственно определяют истинностное значение получающегося сложного предложения. В свою очередь, в качестве Л рассматриваются подчас и такие связки, содержательные аналоги которых в обычном языке, как правило, не имеют специальных наименований; таков, например, "штрих Шеффера" ½ в нижеследующей таблице, где приведен полный перечень всех 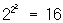 двуместных пропозициональных Л (в первых двух столбцах помещены истинностные значения некоторых "исходных" высказываний р и q, в остальных - значения высказываний, образуемых из них посредством указанных сверху Л). двуместных пропозициональных Л (в первых двух столбцах помещены истинностные значения некоторых "исходных" высказываний р и q, в остальных - значения высказываний, образуемых из них посредством указанных сверху Л).
|
Тождественная истина
|
Тождественная ложь
|
|
Отррицание p
|
q
|
Отрицание q
|
Конъюнкция
|
Антиконъюнкция (штрих Шеффера)
|
Дизъюнкция
|
Антидизъюнкция
|
Эквиваленция
|
Антиэквиваленция
|
Импликация
|
Антиимпликация
|
Обратная импликация
|
Обратная антиимпликация
|
p
|
q
|
и
|
л
|
p
|
ù p
|
q
|
ù q
|
p&q
|
÷q
|
pÚq
|
p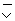 q q
|
p~q
|
p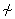 q q
|
pÉq
|
p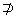 q q
|
pÌq
|
pËq
|
и
|
и
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
л
|
и
|
л
|
и
|
и
|
л
|
л
|
и
|
л
|
и
|
и
|
л
|
л
|
и
|
и
|
л
|
л
|
и
|
и
|
л
|
л
|
и
|
и
|
л
|
л
|
и
|
и
|
л
|
л
|
и
|
л
|
л
|
и
|
л
|
л
|
и
|
л
|
и
|
л
|
и
|
л
|
и
|
и
|
л
|
и
|
л
|
и
|
л
|
Поскольку в таблице сведены все мыслимые двуместные Л, соответствующие всевозможным "четырехбуквенным словам" из "и" и "л", записанным по вертикали в ее столбцах, то естественно, что среди этих 17 Л есть и "вырожденные" случаи: первые две "связки" вообще не зависят ни от каких "аргументов" - это константы "и" и "л" (понятно, что таких "нульместных" связок имеется ровно 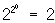 ), далее идут ), далее идут 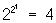 "одноместных связок" (каждая из которых зависит лишь от одного из аргументов р или q) и только затем уже 16-2-4 = 10 собственно двуместных Л Можно далее рассматривать "одноместных связок" (каждая из которых зависит лишь от одного из аргументов р или q) и только затем уже 16-2-4 = 10 собственно двуместных Л Можно далее рассматривать 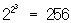 трехместных Л и т. д.; оказывается, однако, что уже небольшой части приведенных Л достаточно для того, чтобы посредством их суперпозиций (т. е. последовательного применения) выразить любые n-местные Л для любого натурального n. Такими функционально полными наборами связок являются, например, ù и &, ù и трехместных Л и т. д.; оказывается, однако, что уже небольшой части приведенных Л достаточно для того, чтобы посредством их суперпозиций (т. е. последовательного применения) выразить любые n-местные Л для любого натурального n. Такими функционально полными наборами связок являются, например, ù и &, ù и 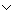 , ù и É и даже одна-единственная связка ½. Поскольку логика высказываний может быть изоморфно (см. Изоморфизм) интерпретирована в терминах логики классов, для каждой Л имеется аналогичная теоретико-множественная операция; совокупность таких операций над множествами (классами) образует т. н. алгебру множеств. См. Алгебра логики. , ù и É и даже одна-единственная связка ½. Поскольку логика высказываний может быть изоморфно (см. Изоморфизм) интерпретирована в терминах логики классов, для каждой Л имеется аналогичная теоретико-множественная операция; совокупность таких операций над множествами (классами) образует т. н. алгебру множеств. См. Алгебра логики.
Лит.: Черч А., Введение в математическую логику, пер. с англ., т. 1, М., 1960, §§ 05, 06 и 15.
Ю. А. Гастев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:55:50
|

|

|
 |
|

|
 |
 |
 |
|