|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Логарифмические таблицы | Логарифмические таблицы (далее Л), таблицы логарифмов чисел; применяются для упрощения вычислений. Наиболее распространены таблицы десятичных логарифмов. Т. к. десятичные логарифмы чисел и 10k (при k целом) различаются только характеристиками и имеют одинаковые мантиссы (lg10k = k + lg ), то в таблицах десятичных логарифмов приводятся только мантиссы логарифмов целых чисел. Для отыскания характеристики служат правила: 1) характеристика числа, большего 1, на единицу меньше числа цифр в целой части этого числа (так, lg 20 000 = 4,30103) и 2) характеристика десятичной дроби, меньшей 1, равна взятому со знаком минус числу нулей, предшествующих первой в дроби цифре, отличной от нуля (так, lg 0,0002 = - 4,30103, т. о., десятичные логарифмы дробей записываются в виде суммы положительной мантиссы и отрицательной характеристики).
Существуют таблицы десятичных логарифмов с различным числом знаков мантисс. Наиболее распространены 4-значные и 5-значные таблицы. Иногда употребляют 7-значные таблицы, а в редких случаях — таблицы, позволяющие без большого труда вычислять логарифмы с большим числом знаков. В Л часто приводятся таблицы антилогарифмов — чисел, логарифмы которых суть данные числа, и таблицы так называемых гауссовых логарифмов, служащих для определения логарифмов суммы или разности двух чисел по известным логарифмам этих чисел (без промежуточного нахождения самих чисел). Кроме логарифмов чисел, Л содержат обычно логарифмы тригонометрических величин.
Первые Л были составлены независимо друг от друга Дж. Непером и швейцарским математиком И. Бюрги. Таблицы Непера "Описание удивительной таблицы логарифмов" (1614) и "Устройство удивительной таблицы логарифмов" (1619) содержали 8-значные логарифмы синусов, косинусов и тангенсов для углов от 0° до 90°, следующих через одну минуту. Т. к. синус 90° тогда принимали равным 107, а на него часто приходилось умножать, то Непер определил свои Л. так, что логарифм 107 был равен нулю. Логарифмы остальных синусов, меньших 107, у него положительны. Непер не ввел понятия об основании системы логарифмов. Его логарифм числа в современных обозначениях приблизительно равен 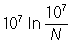 . Свойства логарифмов Непера несколько сложнее обычных, т. к. у него логарифм единицы отличен от нуля.
"Арифметические и геометрические таблицы прогрессий" (1620) Бюрги представляют собой первую таблицу антилогарифмов ("черные числа") и дают значения чисел, соответствующих равноотстоящим логарифмам ("красным числам"). "Красные числа" Бюрги суть логарифмы поделенных на 108 "черных чисел" при основании, равном 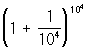 . Таблицы Бюрги и особенно Непера немедленно привлекли внимание математиков к теории и вычислению логарифмов. По совету Непера английский математик Г. Бриге вычислил 8-значные десятичные логарифмы (1617) от 1 до 1000 и затем 14-значные (1624) от 1 до 20 000 и от 90 000 до 100 000 (по его имени десятичные логарифмы иногда называют бриговыми). 10-значные таблицы от 1 до 100 000 издал голландский математик А. Влакк (1628). Таблицы Влакка легли в основу большинства последующих таблиц, причем их авторы внесли много изменений в структуру Л и поправок в выкладки (у самого Влакка было 173 ошибки, у австрийского математика Г. Вега в 1783 — пять; первые безошибочные таблицы выпустил в 1857 немецкий математик К. Бремикер). В России таблицы логарифмов впервые были изданы в 1703 при участии Л. Ф. Магницкого. Таблицы т. н. гауссовых логарифмов были опубликованы в 1802 итальянским математиком З. Леонелли; К. Ф. Гаусс ввел (1812) эти логарифмы в общее употребление.
Лит.: Брадис В. М., Четырехзначные математические таблицы, М. — Л., 1928, посл., 44 изд., М., 1973; Милн-Томсон Л.-М., Комри Л.-Дж., Четырехзначные математические таблицы, пер. с англ., М., 1961; Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М., 1972; Вега Г., Таблицы семизначных логарифмов, 4 изд., М., 1971; Субботин М. Ф., Многозначные таблицы логарифмов, М. — Л., 1940; Десятизначные таблицы логарифмов комплексных чисел..., М., 1952; Таблицы натуральных логарифмов, 2 изд., т. 1—2, М., 1971. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.12.2024 18:04:49
|
|
|
|
|
|
|
|
|
|
|
