
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Логарифм | Логарифм (далее Л) числа по основанию а, показатель степени m, в которую следует возвести число а (основание Л), чтобы получить ; обозначается loga. Итак, m = loga, если ам = . Например, log10 100 = 2; log2 1/32 = - 5; loga 1 = 0, т. к. 100 = 102, 1/32 = 2-5, 1 = a0. При отрицательных а бесконечно много положительных чисел не имело бы действительных логарифмов, поэтому берется а > 0 и а ¹ 1. Из свойств логарифмической функции вытекает, что каждому положительному числу соответствует при данном основании единств. действительный Л (логарифмы отрицательных чисел являются комплексными числами). Основные свойства Л:
loga(MN) = logaM + loga;
logaM/ = logaM - loga;
logak = k loga;
loga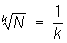 loga loga
позволяют сводить умножение и деление чисел к сложению и вычитанию их Л, а возведение в степень и извлечение корня — к умножению и делению Л на показатель степени или корня, т. е. к более простым действиям.
Когда основание а фиксировано, говорят об определенной системе Л В соответствии с десятичным характером нашего счета наиболее употребительны десятичные Л (а = 10), обозначаемые lg . Для рациональных чисел, отличных от 10k с целым k, десятичные Л суть трансцендентные числа, которые приближенно выражают в десятичных дробях. Целую часть десятичного Л наз. характеристикой, дробную — мантиссой. Так как lg(10k) = k + lgN, то десятичные Л чисел, отличающихся множителем 10k, имеют одинаковые мантиссы и различаются лишь характеристиками. Это свойство лежит в основе построения таблиц Л, которые содержат лишь мантиссы Л целых чисел (см. Лические таблицы).
Большое значение имеют также натуральные Л, основанием которых служит трансцендентное число e = 2,71828...; их обозначают lnN. Переход от одного основания Л к другому совершается по формуле logb = loga/logab, множитель 1/logab называется модулем перехода (перевода) от основания а к основанию b. Для перехода от натуральных Л к десятичным или обратно имеем
lnN = IgN/lge, lgN = /ln10;
1/lge = 2,30258; 1/ln10 = 0,43429....
Историческая справка. Открытие Л было связано в первую очередь с быстрым развитием астрономии в 16 в., уточнением астрономических наблюдений и усложнением астрономических выкладок. Авторы первых таблиц Л исходили из зависимости между свойствами геометрической прогрессии и составленной из показателей степени ее членов арифметической прогрессии. Эти зависимости, частично подмеченные еще Архимедом (3 в. до н. э.), были хорошо известны Н. Шюке (1484) и немецкому математику М. Штифелю (1544). Первые логарифмические таблицы были составлены одновременно и независимо друг от друга Дж. Непером (1614, 1619) и швейцарским математиком И. Бюрги (1620). Важный шаг в теоретическом изучении Л сделал бельгийский математик Григорий из Сен-Винцента (1647), обнаруживший связь Л и площадей, ограниченных дугой гиперболы, осью абсцисс и соответствующими ординатами. Представление Л бесконечным степенным рядом дано Н. Меркатором (1668), нашедшим, что
(1+x) = x 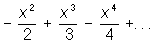
Вскоре затем Дж. Грегори (1668) открыл разложение
ln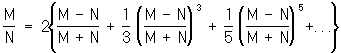 . .
Этот ряд очень быстро сходится, если М = + 1 и достаточно велико; поэтому он может быть использован для вычисления Л В развитии теории Л большое значение имели работы Л Эйлера. Им установлено понятие о логарифмировании как действии, обратном возведению в степень.
Термин "Л" предложил Дж. Непер; он возник из сочетания греческих слов logos (здесь — отношение) и arithmos (число); в античной математике квадрат, куб и т. д. отношения а/b называются "двойным", "тройным" и т. д. отношением. Т. о., для Непера слова "lógu arithmós" означали "число (кратность) отношения", то есть Л у Дж. Непера — вспомогательное число для измерения отношения двух чисел. Термин "натуральный логарифм" принадлежит Н. Меркатору, "характеристика" — английскому математику Г. Бригсу, "мантисса" в нашем смысле — Л Эйлеру, "основание" Л — ему же, понятие о модуле перехода ввел Н. Меркатор. Современное определение Л впервые дано английским математиком В. Гардинером (1742). Знак Л — результат сокращения слова "Л" — встречается в различных видах почти одновременно с появлением первых таблиц (напр., Log — у И. Кеплера (1624) и Г. Бригса (1631), log и 1. — Б. Кавальери (1632, 1643)).
Лит.: Маркушевич А. И., Площади и логарифмы, М. — Л, 1952; История математики, т. 2, М., 1970. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:39:46
|

|

|
 |
|

|
 |
 |
 |
|