
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линии второго порядка | Линии второго порядка (далее Л), плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени
a11x2 + a12xy + a22y2 + 2a13x + 2a23y + a11 = 0. (*)
Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведенных ниже канонических видов, каждому из которых соответствует определенный класс линий. Именно,
нераспадающиеся линии:
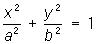 — эллипсы, — эллипсы,
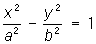 — гиперболы, — гиперболы,
y2 = 2px — параболы,
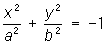 — мнимые эллипсы; — мнимые эллипсы;
распадающиеся линии:
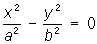 — пары пересекающихся прямых, — пары пересекающихся прямых,
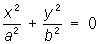 — пары мнимых пересекающихся прямых, — пары мнимых пересекающихся прямых,
x2 - а2 = 0 — пары параллельных прямых,
x2 + а2 = 0 — пары мнимых параллельных прямых,
x2 = 0 — пары совпадающих параллельных прямых.
Исследование вида Л может быть проведено без приведения общего уравнения к каноническому виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов Л — выражений, составленных из коэффициентов уравнения (*), значения которых не меняются при параллельном переносе и повороте системы координат:
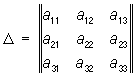 , , 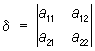 , ,
= a11 + a22, (aij = aji).
Так, например, эллипсы, как нераспадающиеся линии, характеризуются тем, что для них D ¹ 0; положительное значение инварианта d выделяет эллипсы среди других типов нераспадающихся линий (для гипербол d < 0, для парабол d = 0). Различить случаи действительного или мнимого эллипсов позволяет сопоставление знаков инвариантов D и : если D и разных знаков, эллипс действительный; эллипс мнимый, если D и одного знака.
Три основные инварианта D, d и определяют Л (кроме случая параллельных прямых) с точностью до движения евклидовой плоскости: если соответствующие инварианты D, d и двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).
Существуют классификации Л с точки зрения др. групп преобразований. Так, относительно более общей, чем группа движений, — группы аффинных преобразований — эквивалентными являются любые две линии, определяемые уравнениями одного канонического вида. Например, две подобные Л (см. Подобие) считаются эквивалентными. Связи между различными аффинными классами Л позволяет установить классификация с точки зрения проективной геометрии, в которой бесконечно удаленные элементы не играют особой роли. Действительные нераспадающиеся Л: эллипсы, гиперболы и параболы образуют один проективный класс — класс действительных овальных линий (овалов). Действительная овальная линия является эллипсом, гиперболой или параболой в зависимости от того, как она расположена относительно бесконечно удаленной прямой: эллипс пересекает несобственную прямую в двух мнимых точках, гипербола — в двух различных действительных точках, парабола касается несобственной прямой; существуют проективные преобразования, переводящие эти линии одна в другую. Имеется всего 5 проективных классов эквивалентности Л Именно,
невырождающиеся линии
(x1, x2, x3 — однородные координаты):
x12 + x22 — x32 = 0 — действительный овал,
x12 + x22 + x32 = 0 — мнимый овал,
вырождающиеся линии:
x12 — x22 = 0 — пара действительных прямых,
x12 + x22 = 0 — пара мнимых прямых,
x12 = 0 — пара совпадающих действительных прямых.
Кроме аналитического способа определения Л, то есть заданием уравнения, существуют и др. способы. Например, эллипс, гипербола и парабола могут быть получены как сечения конуса плоскостью — конические сечения.
Лит.: Александров П. С., Лекции по аналитической геометрии..., М., 1968; Ефимов Н. В., Краткий курс аналитической геометрии, 5 изд., М., 1960.
А. Б. Иванов. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:49:58
|

|

|
 |
|

|
 |
 |
 |
|