
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линейный функционал | Линейный функционал (далее Л), обобщение понятия линейной формы на линейные пространства. Линейным функционалом f на линейном нормированном пространстве Е называют числовую функцию f(x), определенную для всех х из Е и обладающую следующими свойствами:
1) f(x) линейна, т. е. f((x + (у) = (f(x) + (f(y),
где х и у — любые элементы из Е, a и b — числа;
2) f(x) непрерывна.
Непрерывность f равносильна требованию, чтобы  было ограничено в Е; выражение было ограничено в Е; выражение 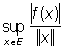 называют нормой f и обозначают называют нормой f и обозначают 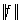 . .
В пространстве С (a, b) функций a(t), непрерывных при a ( t ( b, с нормой 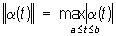 Л являются, например, выражения: Л являются, например, выражения:
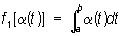 , ,
f2(((t)) = ((t0), a ( t0 ( b.
В гильбертовом пространстве Н Л суть скалярные произведения (l, х), где l — любой фиксированный элемент пространства Н; ими исчерпываются все Л этого пространства.
Во многих задачах можно из общих соображений установить, что та или иная величина является Л Например, к Л приводит решение линейных дифференциальных уравнений с линейными краевыми условиями. Поэтому очень существенным является вопрос об общем аналитическом выражении Л в разных пространствах.
Совокупность всех Л данного пространства Е превращается в линейное нормированное пространство 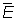 , если определить естественным образом сложение Л и умножение их на числа. Пространство , если определить естественным образом сложение Л и умножение их на числа. Пространство 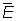 называют сопряженным к называют сопряженным к 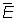 ; это пространство играет большую роль при изучении Е. ; это пространство играет большую роль при изучении Е.
С понятием Л связано понятие слабой сходимости. Последовательность {xn} элементов линейного нормированного пространства называют слабо сходящейся к элементу х, если
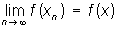
для любого Л f. См. также Функциональный анализ. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:05:48
|

|

|
 |
|

|
 |
 |
 |
|