
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линейное программирование | Линейное программирование (далее Л), математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств; Л является одним из разделов математического программирования.
Типичным представителем задач Л является следующая: найти максимум линейной функции
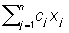 (1) (1)
при условиях
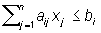 , i = 1, 2, ..., m, (2) , i = 1, 2, ..., m, (2)
xj ³ 0, j = 1, 2, n, (3)
где cj, aij и bi — заданные величины.
Задачи Л являются математическими моделями многочисленных задач технико-экономического содержания. Рассмотрим в качестве примера следующую задачу планирования работы предприятия. Для производства однородных изделий необходимо затратить различные производственные факторы — сырье, рабочую силу, станочный парк, топливо, транспорт и т. д. Обычно имеется несколько отработанных технологических способов производства, причем в этих способах затраты производственных факторов в единицу времени для выпуска изделий различны. Количество израсходованных производственных факторов и количество изготовленных изделий зависит от того, сколько времени предприятие будет работать по тому или иному технологическому способу. Ставится задача рационального распределения времени работы предприятия по различным технологическим способам, т. е. такого, при котором будет произведено максимальное количество изделий при заданных ограниченных затратах каждого производственного фактора. Формализуем задачу. Пусть имеется n технологических способов производства изделий и m производственных факторов. Введем обозначения: cj — количество изделий, выпускаемых в единицу времени при работе по j-му технологическому способу; aij — расход i-го производственного фактора в единицу времени при работе по j-му технологическому способу; bi — имеющиеся ресурсы i-го производственного фактора и xj — планируемое время работы по j-му технологическому способу. Величина
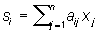
означает общий расход i-го производственного фактора при плане х(i) = (x(i)1, x(i)2, ..., x(i)n). И поскольку ресурсы ограничены величинами bi, то возникают естественные условия (2) и (3). Ставится задача отыскания такого распределения времени (оптимального плана) х* = (x*1, х*2, ..., х* n) работы по каждому технологическому способу, при котором общий объем продукции 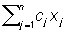 был бы максимальным, то есть задача (1) — (3). Другим характерным примером прикладных задач Л является транспортная задача. был бы максимальным, то есть задача (1) — (3). Другим характерным примером прикладных задач Л является транспортная задача.
Термин "Л" нельзя признать удачным, однако смысл его в том, что в Л решаются задачи составления оптимальной программы (плана) действий. В связи с этим Л можно рассматривать как один из математических методов в исследованиях операций (см. Операций исследование).
Функцию (1) в Л принято называть целевой функцией, или критерием эффективности, вектор х = (x1, x2, ..., xn) — планом, вектор x*=(x*1, x*2, ..., x*n) — оптимальным планом, а множество, определяемое условиями (2) — (3), — допустимым, или множеством планов. Одним из основных методов решения задач Л является симплексный метод. Геометрически его идея состоит в следующем. Допустимое множество (2) — (3) представляет собой выпуклое многогранное множество (если оно ограничено, то — многомерный выпуклый многогранник). Если задача Л имеет решение, то существует вершина х* многогранного множества, являющаяся оптимальным планом. Симплексный метод состоит в таком направленном переборе вершин, при котором значение целевой функции возрастает от вершины к вершине. Каждой вершине соответствует система уравнений, выбираемая спец. образом из системы неравенств (2) — (3), поэтому вычислительная процедура симплексного метода состоит в последовательном решении систем линейных алгебраических уравнений. Простота алгоритма делает этот метод удобным для его реализации на ЭВМ.
Лит.: Юдин Д. Б., Гольштейн Е. Г., Л, М., 1969.
В. Г. Карманов. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:52:12
|

|

|
 |
|

|
 |
 |
 |
|