
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линейного интерполирования метод | Линейного интерполирования метод (далее Л), один из методов приближенного вычисления корней уравнения (трансцендентного или алгебраического) f(x) = 0. Сущность Л заключается в следующем. Исходя из двух близких к корню а значений x0 и x1, в которых функция f(x) принимает значения разных знаков, берут в качестве следующего приближенного значения x2 корня a точку пересечения с осью абсцисс прямой, проходящей через точки (x0, f(x0*( и (x1, f(x1*( (см. рис.). Повторяя эту процедуру на более узком интервале (х0, x2), находят следующее приближение x3 и т. д. Общая формула Л имеет вид
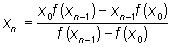 , (n = 2, 3, ...). , (n = 2, 3, ...).
Др. названия Л: метод хорд, метод секущих и (устаревшее) правило ложного положения (Regula faisi).
Лит.: Березин И. С.. Жидков Н. П., Методы вычислений, 2 изд., т. 2, М., 1962.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:38:26
|

|

|
 |
|

|
 |
 |
 |
|