
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линейная зависимость | Линейная зависимость (далее Л)(матем.), соотношение вида
11u1 + 2u2 + ... + nun = 0, (*)
где С1, 2, ..., n — числа, из которых хотя бы одно отлично от нуля, а u1, u2, ..., un — те или иные матем. объекты, для которых определены операции сложения и умножения на число. В соотношение (*) объекты u1, u2, ..., un входят в 1-й степени, т. е. линейно; поэтому описываемая этим соотношением зависимость между ними называется линейной. Знак равенства в формуле (*) может иметь различный смысл и в каждом конкретном случае должен быть разъяснен. Понятие Линейная зависимость употребляется во многих разделах математики. Так, можно говорить о Линейная зависимость между векторами, между функциями от одного или нескольких переменных, между элементами линейного пространства и т. д. Если между объектами u1, u2, ..., un имеется Линейная зависимость, то говорят, что эти объекты линейно зависимы; в противном случае их называется линейно независимыми. Если объекты u1, u2, ..., un линейно зависимы, то хотя бы один из них является линейной комбинацией остальных, т. е.
u1 = a 1u1 + ... + a i-1ui-1 + a i+1ui+1 + ... + a nun.
Непрерывные функции от одного переменного
u1 = j 1(х), u2 = j 2(х), ..., un = j n(x) называются линейно зависимыми, если между ними имеется соотношение вида (*), в котором знак равенства понимается как тождество относительно х. Для того чтобы функции j 1(x), j 2(x), ..., j n(x), заданные на некотором отрезке а £ х £ b, были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль их определитель Грама
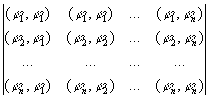
где
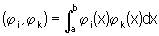
i, k = 1,2, ..., n.
Если же функции j1 (x), j2(x), ..., jn(x) являются решениями линейного дифференциального уравнения, то для существования Линейная зависимость между ними необходимо и достаточно, чтобы вронскиан обращался в нуль хотя бы в одной точке.
Линейные формы от m переменных
u1 = ai1x1 + ai2x2 + ... + aimxm
(i = 1, 2, ..., n)
называются линейно зависимыми, если существует соотношение вида (*), в котором знак равенства понимается как тождество относительно всех переменных x1, x2, ..., xm. Для того чтобы n линейных форм от n переменных были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль определитель
D= 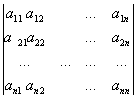 |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:10:32
|

|

|
 |
|

|
 |
 |
 |
|