
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Лежандра многочлены | Лежандра многочлены (далее Л), сферические многочлены, специальная система многочленов последовательно возрастающих степеней. Впервые рассматривалась А. Лежандром и П. Лапласом (в 1782—85) независимо друг от друга. Для n = 0,1,2,... Л Р (х) могут быть определены формулой:
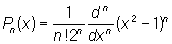 , ,
в частности:
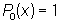 , , 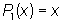 , , 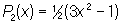 , ,
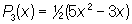 , ,
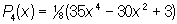 , ,
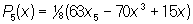
и т.д. Все нули многочлена n (x) — действительные и лежат в основном промежутке (—1, +1), перемежаясь с нулями многочлена n+i (x). Л — ортогональные многочлены с весом 1 на отрезке (—1, +1,); они образуют полную систему, чем обусловливается возможность разложения в ряд по Л произвольной функции f (x), интегрируемой на отрезке (—1, +1):
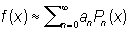 , ,
где 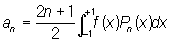 . .
Характер сходимости рядов по Л примерно тот же, что и рядов Фурье.
Явное выражение для Л:
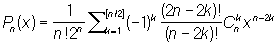 . .
Производящая функция:
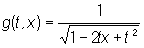
(Л — коэффициенты при n-й степени в разложении этой функции по степеням t). Рекуррентная формула:
nPn (x) + (n - 1) n-2(x) - (2n - 1) xPn-1(x) = 0.
Дифференциальное уравнение для Л
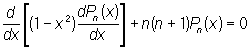
возникает при разделении переменных в уравнении Лапласа в сферических координатах. См. также Сферические функции.
Лит.: Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968; Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М. — Л., 1963.
В. Н. Битюцков. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:03:09
|

|

|
 |
|

|
 |
 |
 |
|