|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Лапласа уравнение | Лапласа уравнение (далее Л), дифференциальное уравнение с частными производными
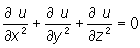
где х, у, z — независимые переменные, а u = u(x, y, z) — искомая функция. Это уравнение названо по имени П. Лапласа, рассмотревшего его в работах по теории тяготения (1782). К Л приводит ряд задач физики и техники. Л удовлетворяют температура при стационарных процессах, потенциал электростатического поля в точках пространства, свободных от зарядов, потенциал поля тяготения в области, не содержащей притягивающих масс, и т. п. Функции, удовлетворяющие Л, называются гармоническими функциями. О постановке задач для Л см. в ст. Краевые задачи. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.02.2025 16:00:23
|
|
|
|
|
|
|
|
|
|
|
