
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Лапласа теорема | Лапласа теорема (далее Л), простейшая из предельных теорем теории вероятностей, относящаяся к распределению отклонений частоты появления события при независимых испытаниях от его вероятности. В общем виде эта теорема доказана П. Лапласом в книге "Аналитическая теория вероятностей" (1812). Один частный случай Л был известен А. Муавру (1730), в связи с чем Л иногда называется теоремой Муавра — Лапласа. Формулировка Л такова. Пусть при каждом из n независимых испытаний вероятность появления некоторого события Е равна р (0<р<1) и пусть m обозначает число испытаний, в которых событие Е фактически наступает; тогда вероятность неравенства
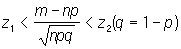
при достаточно большом числе испытаний n сколь угодно мало отличается от
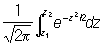 . .
Если обозначить через Xk случайную величину, принимающую значение, равное 1, при появлении события Е в k-ом испытании и значение, равное 0, при его непоявлении, то m представляется как сумма независимых случайных величин m = X1 + ...+ Xn. Это позволяет рассматривать Л как частный случай более общих предельных теорем теории вероятностей, в частности Ляпунова теоремы.
Приближенные значения вероятностей, даваемые Л, на практике используются как точные при npq порядка нескольких десятков и большем.
Лит. см. при ст. Предельные теоремы теории вероятностей.
Ю. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:39:21
|

|

|
 |
|

|
 |
 |
 |
|