
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Лапласа преобразование | Лапласа преобразование (далее Л), преобразование, переводящее функцию f (t) действительного переменного t (0 < t < ¥), называемую "оригиналом", в функцию
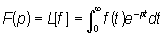 (1) (1)
комплексного переменного р =s +it. Под Л понимают также не только само преобразование, но и его результат — функцию (p). Интеграл в правой части формулы (1) называется интегралом Лапласа. Он был рассмотрен П. Лапласом в ряде работ, которые объединены в его книге "Аналитическая теория вероятностей", вышедшей в 1812. Значительно раньше (в 1737) такие интегралы применял к решению дифференциальных уравнений Л. Эйлер.
При некоторых условиях, указанных ниже, Л определяет функцию f (t) однозначно, в простейших случаях — по формуле обращения:
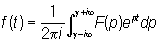 (2) (2)
Л является линейным функциональным преобразованием. Из числа основных формул Л можно отметить следующие:
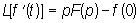 , ,
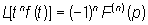 , n = 1, 2, …, , n = 1, 2, …,
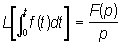 , t >0. , t >0.
Л в сочетании с формулой (2) его обращения применяется к интегрированию дифференциальных уравнений. В частности, в силу свойства (1) и линейности, Л решения обыкновенного линейного дифференциального уравнения с постоянными коэффициентами удовлетворяет алгебраическому уравнению 1-й степени и может быть, следовательно, легко найдено. Так, если, например, у" + у = f (t), y (0) = y` (0) = 0
и (p) = L (y), (p) = L (f),
то L (y") = p2 (p)
и p2 (p) + (p) = (p),
откуда
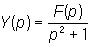
Многочисленные задачи электротехники, гидродинамики, механики, теплопроводности эффективно решаются методами, использующими Л
Л нашло особенно широкое применение в обосновании операционного исчисления, в котором обычно вместо Л (p) вводится "изображение" оригинала f (t) — функция pF (p).
Современная общая теория Л строится на основе интегрирования в смысле Лебега (см. Интеграл). Для применимости Л к функции f (t) необходимо, чтобы f (t) была интегрируема в смысле Лебега на любом конечном интервале (0, t), t > 0 и интеграл (1) для нее сходился хотя бы в одной точке p0 = s0 + it0. Если интеграл (1) сходится в точке р0, то он сходится во всех точках р, для которых (р—р0) > 0. Т. о., если интеграл (1) сходится хотя бы в одной точке плоскости p0, то либо он сходится во всей плоскости, либо существует такое число sс, что при p > sc интеграл (1) сходится, а при р < sс расходится. Число sс называется абсциссой сходимости интеграла Лапласа. (p) — аналитическая функция в полуплоскости р > sс.
Лит.: Диткин В. А. и Кузнецов П. И., Справочник по операционному исчислению. Основы теории и таблицы формул, М. — Л., 1951; Диткин В. А. и Прудников А. П., Интегральные преобразования и операционное исчисление, М., 1961; Деч Г., Руководство к практическому применению преобразования Лапласа, пер. с нем., М., 1965. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:39:55
|

|

|
 |
|

|
 |
 |
 |
|