
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Лагранжа функция | Лагранжа функция (далее Л) кинетический потенциал, характеристическая функция L(qi, 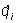 , t) механической системы, выраженная через обобщенные координаты qi, обобщенные скорости , t) механической системы, выраженная через обобщенные координаты qi, обобщенные скорости 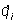 и время t. В простейшем случае консервативной системы Л равна разности между кинетической Т и потенциальной П энергиями системы, выраженными через qi и и время t. В простейшем случае консервативной системы Л равна разности между кинетической Т и потенциальной П энергиями системы, выраженными через qi и 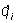 , т. е. L = T(qi, , т. е. L = T(qi, 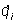 , t) - П(qi). Зная Л, можно с помощью наименьшего действия принципа составить дифференциальные уравнения движения механической системы. , t) - П(qi). Зная Л, можно с помощью наименьшего действия принципа составить дифференциальные уравнения движения механической системы. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:12:04
|

|

|
 |
|

|
 |
 |
 |
|