
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Лагранжа метод множителей | Лагранжа метод множителей (далее Л)метод решения задач на условный экстремум; Лагранжа метод множителей заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.
Для задачи об экстремуме функции f (х1, x2,..., xn) при условиях (уравнениях связи) ji(x1, x2, ..., xn) = 0, i = 1, 2,..., m, функция Лагранжа имеет вид
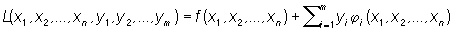 . .
Множители y1, y2, ..., ym наз. множителями Лагранжа.
Если величины x1, x2, ..., xn, y1, y2, ..., ym суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений
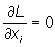 , i = 1, …, n; , i = 1, …, n; 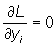 , i = 1, …,m, , i = 1, …,m,
то при достаточно общих предположениях x1, x2, ..., xn доставляют экстремум функции f. Функция Лагранжа L применяется также при исследовании задач вариационного исчисления и математического программирования. Впервые Лагранжа метод множителей был предложен в 1797 Ж. Лагранжем в связи с задачами дифференциального исчисления.
Лит.: Кудрявцев Л. Д., Математический анализ, т. 2, М., 1970. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:14:30
|

|

|
 |
|

|
 |
 |
 |
|