|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Лагерра многочлены | Лагерра многочлены (далее Л) (по имени французского математика Э. Лагерра, Е. Laguerre; 1834—86), специальная система многочленов последовательно возрастающих степеней. Для n = 0, 1, 2 ... Л Ln(x) могут быть определены формулой:
 ;
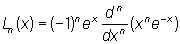в частности:
L0(x) = 1, L1(x) = x - 1, L2(x) = x2 - 4x + 2, L3(x) = x3 - 9x2 + 18x - 6.
Л ортогональны (см. Ортогональные многочлены) на полупрямой х ³ 0 относительно веса е-х. Дифференциальное уравнение:
ху" + (1 — х)у` + ny = 0.
Рекуррентная формула:
Ln+1(x) = (x - 2n - 1)Ln(x) - n2Ln-1(x).
Лит.: Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М. — Л., 1963. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 11:08:58
|
|
|
|
|
|
|
|
|
|
|
