
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Координаты (математ.) | Координаты (далее К) (от лат. co (cum) — совместно и ordinatus — упорядоченный, определенный), числа, заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. Первыми вошедшими в систематическое употребление К (математ.) являются астрономические и географические К (математ.) — широта и долгота, определяющие положение точки на небесной сфере или на поверхности земного шара (см. Небесные координаты, Географические координаты). В 14 в. французский математик Н. Орем пользовался К (математ.) на плоскости для построения графиков, называя долготой и широтой то, что теперь называют абсциссой и ординатой. Более систематически К (математ.) стали применяться к вопросам геометрии на плоскости в 17 в. Заслуга выяснения всего значения метода К (математ.), позволяющего систематически переводить задачи геометрии на язык математического анализа и, обратно, истолковывать геометрически факты анализа, принадлежит французскому ученому Р. Декарту. Кроме К (математ.) точки, рассматривают также К (математ.) прямой, плоскости и других геометрических объектов. В теоретической механике употребляют К (математ.) механических систем — числа, определяющие положение механической системы (например, некоторого твердого тела) в каждый момент времени.
К точки на плоскости. Аффинные, или общие декартовы, К (математ.) точки на плоскости получают, выбирая точку О (начало К (математ.)) и два не лежащих на одной прямой вектора 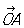 и и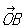 , исходящих из точки О. Положение точки Р определяется (в выбранной системе К (математ.)) двумя К (математ.): абсциссой , исходящих из точки О. Положение точки Р определяется (в выбранной системе К (математ.)) двумя К (математ.): абсциссой
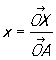
и ординатой
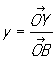 , ,
где XP параллельно и параллельно ОА. В частном случае, когда векторы 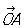 и и 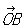 перпендикулярны и имеют одну и ту же длину, получают наиболее употребительные прямоугольные К (математ.) Если угол между перпендикулярны и имеют одну и ту же длину, получают наиболее употребительные прямоугольные К (математ.) Если угол между 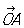 и и 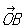 произволен, но длины этих векторов одинаковы, то получают те косоугольные К (математ.), рассмотрением которых ограничивался сам Декарт (часто только их и называют декартовыми, сохраняя для общих декартовых К (математ.) название аффинные К (математ.)). произволен, но длины этих векторов одинаковы, то получают те косоугольные К (математ.), рассмотрением которых ограничивался сам Декарт (часто только их и называют декартовыми, сохраняя для общих декартовых К (математ.) название аффинные К (математ.)).
Полярные К (математ.) точки на плоскости получают, выбирая точку О (полюс). выходящий из нее луч и единицу измерения длин. Координатами точки Р служат расстояние r = н угол j = Ð. Чтобы получить возможность поставить в соответствие каждой точке плоскости Р пару чисел (r, j), достаточно рассматривать r и j, подчиненные неравенствам 0 £r<¥, 0£j<2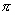 . За исключением точки О, для которой r = 0, а угол j не определен, соответствие между точками Р, отличными от О, и парами (r, j), подчиненными указанным условиям, взаимно однозначно. . За исключением точки О, для которой r = 0, а угол j не определен, соответствие между точками Р, отличными от О, и парами (r, j), подчиненными указанным условиям, взаимно однозначно.
Из других специальных систем К (математ.) на плоскости следует отметить также эллиптические координаты.
В случае аффинных К (математ.) линии х= const образуют пучок прямых, параллельных оси Oy, а линии у = const — другой пучок прямых, параллельных оси Ox, через каждую точку плоскости Р (х0, у0) проходит одна прямая первого пучка (х = x0) и одна прямая второго пучка (у = y0). В случае полярных К (математ.) линии r = const являются окружностями, а линии j = const — лучами, выходящими из начальной точки О; через каждую точку Р, отличную от О, проходит ровно по одной линии каждого из двух семейств; отметки r0 и j0 этих двух линий и являются К (математ.) точки Р. В более общем случае можно рассмотреть в какой-либо области G плоскости две функции точки u (Р) и u() такого рода, что каждая линия u (Р) = const пересекается с каждой линией семейства u() = const в пределах области G не более чем в одной точке. Очевидно, что в этом случае числа u (Р) и u(Р) однозначно определяют положение точки Р в области G, т. е. являются К (математ.) точки Р в этой области; линии, определяемые уравнениями u = const или u = const, называют при этом координатными линиями.
Криволинейные координаты на поверхности. Изложенная идея применима без всяких изменений и к введению криволинейных К (математ.) на произвольной поверхности. Например, для случая долготы j и широты q на сфере линиями j = const являются меридианы, а линиями q = const — широтные круги, расположение которых всем хорошо известно из элементов географии. Криволинейные, или, как их иначе называют, гауссовы, К (математ.) на произвольной поверхности являются основным аппаратом дифференциальной геометрии поверхностей.
Однородные координаты на плоскости. Евклидова плоскость, дополненная бесконечно удаленными элементами, может рассматриваться с проективной точки зрения как замкнутая поверхность (см. Проективная плоскость), на которой бесконечно удаленные точки не играют какой-либо особой роли. На всей проективной плоскости введение К (математ.), характеризующих положение точки парой чисел (u, u) с сохранением взаимной однозначности и непрерывности соответствия, невозможно. Вместо этого пользуются однородными К (математ.) При этом каждой точке ставятся в соответствие не пары, а тройки чисел (x1, x2, x3), причем двум тройкам (x1, x2, x3) и (x1`, x2`, x3`) соответствует одна и та же точка только тогда, когда входящие в них числа пропорциональны, т. е. существует такой множитель l, что
x1` = lx1, x2` = lx2, x3` = lx3.
Такие системы координат играют большую роль в геометрии.
К точки в пространстве. Аффинные, или общие декартовы, К (математ.) в трехмерном пространстве вводятся заданием точки О и трех векторов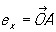 , , 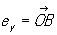 , ,  , не лежащих в одной плоскости. Для получения К (математ.) х, у, z точки Р вектор , не лежащих в одной плоскости. Для получения К (математ.) х, у, z точки Р вектор 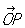 представляют в виде представляют в виде
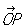 = xex+ уеу+zez. = xex+ уеу+zez.
В простейшем случае прямоугольных К (математ.) векторы ex, еу, ez попарно перпендикулярны и имеют единичную длину. В пространстве возможны два существенно различных типа систем прямоугольных К (математ.): правая система (где еу и ez лежат в плоскости чертежа, а ex направлен вперед, к читателю) и левая система (где ex и ez лежат в плоскости чертежа, а еу направлен к читателю).
В пространстве пользуются также системами криволинейных К (математ.), общая схема которых такова: в какой-либо области G пространства рассматриваются три функции точки u (), u(), w(), подчиненные условию, чтобы через каждую точку Р области G проходила одна поверхность семейства u = const, одна поверхность семейства u = const и одна поверхность семейства w = const. Тем самым каждой точке ставятся в соответствие три числа (u, u, w) — ее К (математ.) Поверхности, определяемые уравнениями u = const, или u = const, или w = const, называют координатными.
В приложениях (к механике, математической физике и пр.) наиболее употребительны некоторые специальные системы криволинейных К (математ.), а именно: сферические координаты, цилиндрические координаты.
К прямой, плоскости и т. п. Принцип двойственности (см. Двойственности принцип), устанавливающий равноправность точек и прямых в геометрии двух измерений и равноправность точек и плоскостей в геометрии трех измерений, подсказывает ту мысль, что с помощью особых К (математ.) могут быть определены положения прямых и плоскостей. Действительно, если, например, в прямоугольных К (математ.) уравнение прямой (не проходящей через начало К (математ.)) приведено к виду ux + uy + 1 = 0, то числами u и u (u = -1/a, u = -1/b, где а и b суть "отрезки", отсекаемые прямой на осях) вполне определяется положение прямой; можно принять (u, u) за К (математ.) (так называемые тангенциальные К (математ.)) прямой линии. Симметричность уравнения ux + uy + 1 = 0 относительно пар (х, у) и (u, u) является аналитическим выражением принципа двойственности. Вполне аналогично случаям n = 2 (плоскость, поверхность) и n = 3 (трехмерное пространство) употребление К (математ.) в n-мepном пространстве.
Лит. см. при ст. Аналитическая геометрия.
А. Н. Колмогоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:55:38
|

|

|
 |
|

|
 |
 |
 |
|